Tutorial: optimal piecewise binning with binary target¶
Basic¶
To get us started, let’s load a well-known dataset from the UCI repository and transform the data into a pandas.DataFrame.
[1]:
import numpy as np
import pandas as pd
from sklearn.datasets import load_breast_cancer
from sklearn.ensemble import GradientBoostingClassifier
[2]:
data = load_breast_cancer()
df = pd.DataFrame(data.data, columns=data.feature_names)
We choose a variable to discretize and the binary target.
[3]:
variable = "mean radius"
x = df[variable].values
y = data.target
Import and instantiate an OptimalPWBinning object class and we pass the variable name. The OptimalPWBinning can ONLY handle numerical variables. This differs from the OptimalBinning object class.
[4]:
from optbinning import OptimalPWBinning
[5]:
optb = OptimalPWBinning(name=variable)
We fit the optimal binning object with arrays x and y. We set a minimum (lower bound) and maximum (upper bound) probability using arguments lb and ub. Note that these bounds are optional, but guarantee an event rate between \([0, 1]\) as any probability distribution. As shown later, settings these bounds will increase the problem size thus leading to higher solution times. An alternative approach to bypass these bounds is implemented when transforming to event rate or WoE
using functions fit and fit_transform, where values outside the interval \([0, 1]\) are clipped.
Note that the Weight-of-Evidence is not defined for event rate equal 0 or 1. Therefore, for small datasets, we recommend modifying the interval \([0, 1]\) with a small value, thus using \([\epsilon, 1 - \epsilon]\).
[6]:
optb.fit(x, y, lb=0.001, ub=0.999)
[6]:
OptimalPWBinning(estimator=LogisticRegression(), name='mean radius')
You can check if an optimal solution has been found via the status attribute:
[7]:
optb.status
[7]:
'OPTIMAL'
You can also retrieve the optimal split points via the splits attribute:
[8]:
optb.splits
[8]:
array([11.42500019, 12.32999992, 13.09499979, 13.70499992, 15.04500008,
16.92500019])
The binning table¶
The optimal binning algorithms return a binning table; a binning table displays the binned data and several metrics for each bin. Class OptimalPWBinning returns an object PWBinningTable via the binning_table attribute.
[9]:
binning_table = optb.binning_table
[10]:
type(binning_table)
[10]:
optbinning.binning.piecewise.binning_statistics.PWBinningTable
The binning_table is instantiated, but not built. Therefore, the first step is to call the method build, which returns a pandas.DataFrame.
[11]:
binning_table.build()
[11]:
| Bin | Count | Count (%) | Non-event | Event | c0 | c1 | |
|---|---|---|---|---|---|---|---|
| 0 | (-inf, 11.43) | 118 | 0.207381 | 3 | 115 | 1.032648 | -0.004820 |
| 1 | [11.43, 12.33) | 79 | 0.138840 | 3 | 76 | 1.644838 | -0.058403 |
| 2 | [12.33, 13.09) | 68 | 0.119508 | 7 | 61 | 2.140569 | -0.098609 |
| 3 | [13.09, 13.70) | 49 | 0.086116 | 10 | 39 | 2.914961 | -0.157745 |
| 4 | [13.70, 15.05) | 83 | 0.145870 | 28 | 55 | 4.105273 | -0.244597 |
| 5 | [15.05, 16.93) | 54 | 0.094903 | 44 | 10 | 3.562495 | -0.208520 |
| 6 | [16.93, inf) | 118 | 0.207381 | 117 | 1 | 0.082142 | -0.002887 |
| 7 | Special | 0 | 0.000000 | 0 | 0 | 0.000000 | 0.000000 |
| 8 | Missing | 0 | 0.000000 | 0 | 0 | 0.000000 | 0.000000 |
| Totals | 569 | 1.000000 | 212 | 357 | - | - |
Let’s describe the columns of this binning table:
Bin: the intervals delimited by the optimal split points.
Count: the number of records for each bin.
Count (%): the percentage of records for each bin.
Non-event: the number of non-event records \((y = 0)\) for each bin.
Event: the number of event records \((y = 1)\) for each bin.
\(c_0\): the first coefficient of the event rate polynomial.
\(c_1\): the second coefficient of the event rate polynomial.
The event rate for bin \(i\) is defined as \(ER_i = c_0 + c_1 x_i\), where \(x_i \in \text{Bin}_{i}\). In general, \begin{equation} ER_i = \sum_{j=0}^d c_j x_i^j, \end{equation} where \(d\) is the degree of the event rate polynomial.
The last row shows the total number of records, non-event records, event records.
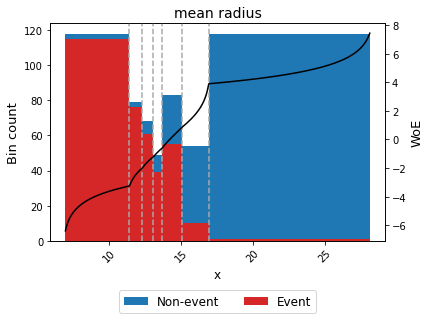
You can use the method plot to visualize the number of non-event and event records by bin, and WoE or event rate curve.
[12]:
binning_table.plot(metric="woe")
[13]:
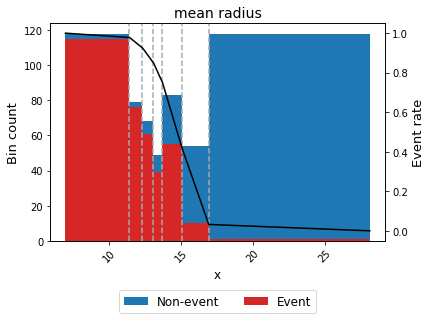
binning_table.plot(metric="event_rate")
Event rate / WoE transformation¶
Now that we have checked the binned data, we can transform our original data into WoE or event rate values.
[14]:
x_transform_woe = optb.transform(x, metric="woe")
[15]:
x_transform_event_rate = optb.transform(x, metric="event_rate")
Advanced¶
Optimal binning Information¶
The OptimalPWBinning can print overview information about the options settings, problem statistics, and the solution of the computation. By default, print_level=1.
[16]:
optb = OptimalPWBinning(name=variable)
optb.fit(x, y)
[16]:
OptimalPWBinning(estimator=LogisticRegression(), name='mean radius')
If print_level=0, a minimal output including the header, variable name, status, and total time are printed.
[17]:
optb.information(print_level=0)
optbinning (Version 0.19.0)
Copyright (c) 2019-2024 Guillermo Navas-Palencia, Apache License 2.0
Name : mean radius
Status : OPTIMAL
Time : 0.1388 sec
If print_level>=1, statistics on the pre-binning phase and the solver are printed. More detailed timing statistics are also included.
[18]:
optb.information(print_level=1)
optbinning (Version 0.19.0)
Copyright (c) 2019-2024 Guillermo Navas-Palencia, Apache License 2.0
Name : mean radius
Status : OPTIMAL
Pre-binning statistics
Number of bins 7
Solver statistics
Type auto
Number of variables 14
Number of constraints 20
Timing
Total time 0.14 sec
Pre-processing 0.00 sec ( 0.79%)
Estimator 0.02 sec ( 16.14%)
Pre-binning 0.08 sec ( 58.47%)
Solver 0.02 sec ( 14.94%)
Post-processing 0.01 sec ( 8.97%)
If print_level=2, the list of all options of the OptimalBinning are displayed.
[19]:
optb.information(print_level=2)
optbinning (Version 0.19.0)
Copyright (c) 2019-2024 Guillermo Navas-Palencia, Apache License 2.0
Begin options
name mean radius * U
estimator yes * U
objective l2 * d
degree 1 * d
continuous True * d
prebinning_method cart * d
max_n_prebins 20 * d
min_prebin_size 0.05 * d
min_n_bins no * d
max_n_bins no * d
min_bin_size no * d
max_bin_size no * d
monotonic_trend auto * d
n_subsamples no * d
max_pvalue no * d
max_pvalue_policy consecutive * d
outlier_detector no * d
outlier_params no * d
user_splits no * d
special_codes no * d
split_digits no * d
solver auto * d
h_epsilon 1.35 * d
quantile 0.5 * d
regularization no * d
reg_l1 1.0 * d
reg_l2 1.0 * d
random_state no * d
verbose False * d
End options
Name : mean radius
Status : OPTIMAL
Pre-binning statistics
Number of bins 7
Solver statistics
Type auto
Number of variables 14
Number of constraints 20
Timing
Total time 0.14 sec
Pre-processing 0.00 sec ( 0.79%)
Estimator 0.02 sec ( 16.14%)
Pre-binning 0.08 sec ( 58.47%)
Solver 0.02 sec ( 14.94%)
Post-processing 0.01 sec ( 8.97%)
Binning table statistical analysis¶
The analysis method performs a statistical analysis of the binning table, computing the statistics Gini index, Information Value (IV), Jensen-Shannon divergence, and the quality score. Additionally, several statistical significance tests between consecutive bins of the contingency table are performed: a frequentist test using the Chi-square test or the Fisher’s exact test, and a Bayesian A/B test using the beta distribution as a conjugate prior of the Bernoulli distribution. The piecewise
binning also includes two performance metrics: the average precision and the Brier score.
[20]:
binning_table.analysis(pvalue_test="chi2")
---------------------------------------------
OptimalBinning: Binary Binning Table Analysis
---------------------------------------------
General metrics
Gini index 0.87503303
IV (Jeffrey) 4.47808383
JS (Jensen-Shannon) 0.37566007
Hellinger 0.44267978
Triangular 1.20862649
KS 0.72390466
Avg precision 0.95577179
Brier score 0.08956351
HHI 0.15727342
HHI (normalized) 0.05193260
Cramer's V 0.80066760
Quality score 0.00000000
Significance tests
Bin A Bin B t-statistic p-value P[A > B] P[B > A]
0 1 0.289789 5.903557e-01 0.697563 3.024368e-01
1 2 2.285355 1.306002e-01 0.941469 5.853092e-02
2 3 2.317546 1.279217e-01 0.936661 6.333919e-02
3 4 2.539025 1.110634e-01 0.950869 4.913141e-02
4 5 29.418844 5.830790e-08 1.000000 1.898148e-11
5 6 18.624518 1.591604e-05 0.999997 3.106835e-06
[21]:
binning_table.analysis(pvalue_test="fisher")
---------------------------------------------
OptimalBinning: Binary Binning Table Analysis
---------------------------------------------
General metrics
Gini index 0.87503303
IV (Jeffrey) 4.47808383
JS (Jensen-Shannon) 0.37566007
Hellinger 0.44267978
Triangular 1.20862649
KS 0.72390466
Avg precision 0.95577179
Brier score 0.08956351
HHI 0.15727342
HHI (normalized) 0.05193260
Cramer's V 0.80066760
Quality score 0.00000000
Significance tests
Bin A Bin B odd ratio p-value P[A > B] P[B > A]
0 1 0.660870 6.855009e-01 0.697563 3.024368e-01
1 2 0.343985 1.879769e-01 0.941469 5.853092e-02
2 3 0.447541 1.829850e-01 0.936661 6.333919e-02
3 4 0.503663 1.153088e-01 0.950869 4.913141e-02
4 5 0.115702 3.464724e-08 1.000000 1.898159e-11
5 6 0.037607 4.144258e-05 0.999997 3.106835e-06
Event rate / WoE monotonicity¶
The monotonic_trend option permits forcing a monotonic trend to the event rate curve. The default setting “auto” should be the preferred option, however, some business constraints might require to impose different trends. The default setting “auto” chooses the monotonic trend most likely to maximize the information value from the options “ascending”, “descending”, “peak” and “valley” using a machine-learning-based classifier. For this example, we choose Gradient Boosting as an estimator.
[22]:
variable = "mean texture"
x = df[variable].values
y = data.target
[23]:
optb = OptimalPWBinning(name=variable, estimator=GradientBoostingClassifier())
optb.fit(x, y, lb=0.001, ub=0.999)
[23]:
OptimalPWBinning(estimator=GradientBoostingClassifier(), name='mean texture')
[24]:
binning_table = optb.binning_table
binning_table.build()
[24]:
| Bin | Count | Count (%) | Non-event | Event | c0 | c1 | |
|---|---|---|---|---|---|---|---|
| 0 | (-inf, 15.05) | 92 | 0.161687 | 4 | 88 | 0.931559 | -0.000000 |
| 1 | [15.05, 16.39) | 61 | 0.107206 | 8 | 53 | 2.075856 | -0.076058 |
| 2 | [16.39, 17.03) | 29 | 0.050967 | 6 | 23 | 2.149343 | -0.080541 |
| 3 | [17.03, 18.46) | 79 | 0.138840 | 17 | 62 | 1.113801 | -0.019751 |
| 4 | [18.46, 19.47) | 55 | 0.096661 | 20 | 35 | 4.139955 | -0.183682 |
| 5 | [19.47, 20.20) | 36 | 0.063269 | 18 | 18 | 4.417900 | -0.197957 |
| 6 | [20.20, 21.71) | 72 | 0.126538 | 43 | 29 | 0.933420 | -0.025416 |
| 7 | [21.71, 22.74) | 40 | 0.070299 | 27 | 13 | 2.611200 | -0.102697 |
| 8 | [22.74, 24.00) | 29 | 0.050967 | 24 | 5 | 0.275868 | -0.000000 |
| 9 | [24.00, 26.98) | 43 | 0.075571 | 30 | 13 | -1.111299 | 0.057799 |
| 10 | [26.98, inf) | 33 | 0.057996 | 15 | 18 | 0.448108 | 0.000000 |
| 11 | Special | 0 | 0.000000 | 0 | 0 | 0.000000 | 0.000000 |
| 12 | Missing | 0 | 0.000000 | 0 | 0 | 0.000000 | 0.000000 |
| Totals | 569 | 1.000000 | 212 | 357 | - | - |
[25]:
binning_table.plot(metric="event_rate")
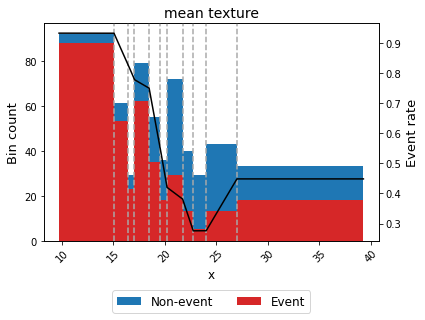
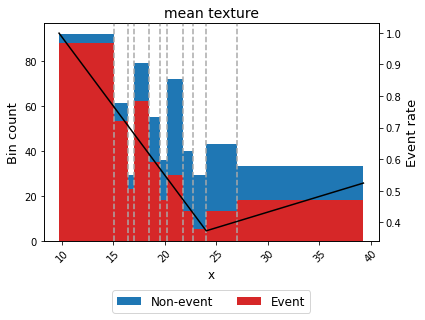
For example, we can force the variable mean texture to be convex with respect to the probability of having breast cancer.
[26]:
optb = OptimalPWBinning(name=variable, estimator=GradientBoostingClassifier(),
monotonic_trend="convex")
optb.fit(x, y, lb=0.001, ub=0.999)
[26]:
OptimalPWBinning(estimator=GradientBoostingClassifier(),
monotonic_trend='convex', name='mean texture')
[27]:
binning_table = optb.binning_table
binning_table.build()
binning_table.plot(metric="event_rate")
User-defined split points¶
In some situations, we have defined split points or bins required to satisfy a priori belief, knowledge or business constraint. The OptimalPWBinning permits to pass user-defined split points. The supplied information is used as a pre-binning, disallowing any pre-binning method set by the user. Furthermore, version 0.5.0 introduces user_splits_fixed parameter, to allow the user to fix some user-defined splits, so these must appear in the solution.
Example numerical variable:
[28]:
user_splits = [ 14, 15, 16, 17, 20, 21, 22, 27]
user_splits_fixed = [False, True, True, False, False, False, False, False]
[29]:
optb = OptimalPWBinning(name=variable, user_splits=user_splits,
user_splits_fixed=user_splits_fixed)
optb.fit(x, y)
[29]:
OptimalPWBinning(estimator=LogisticRegression(), name='mean texture',
user_splits=[14, 15, 16, 17, 20, 21, 22, 27],
user_splits_fixed=[False, True, True, False, False, False,
False, False])
[30]:
binning_table = optb.binning_table
binning_table.build()
[30]:
| Bin | Count | Count (%) | Non-event | Event | c0 | c1 | |
|---|---|---|---|---|---|---|---|
| 0 | (-inf, 14.00) | 54 | 0.094903 | 2 | 52 | 1.154009 | -0.020568 |
| 1 | [14.00, 15.00) | 37 | 0.065026 | 2 | 35 | 1.353911 | -0.034847 |
| 2 | [15.00, 16.00) | 43 | 0.075571 | 7 | 36 | 1.247073 | -0.027725 |
| 3 | [16.00, 20.00) | 210 | 0.369069 | 59 | 151 | 1.569012 | -0.047846 |
| 4 | [20.00, 21.00) | 45 | 0.079086 | 26 | 19 | 1.937897 | -0.066290 |
| 5 | [21.00, 22.00) | 49 | 0.086116 | 30 | 19 | 1.543738 | -0.047520 |
| 6 | [22.00, 27.00) | 99 | 0.173989 | 71 | 28 | 1.893765 | -0.063431 |
| 7 | [27.00, inf) | 32 | 0.056239 | 15 | 17 | 0.181134 | 0.000000 |
| 8 | Special | 0 | 0.000000 | 0 | 0 | 0.000000 | 0.000000 |
| 9 | Missing | 0 | 0.000000 | 0 | 0 | 0.000000 | 0.000000 |
| Totals | 569 | 1.000000 | 212 | 357 | - | - |
[31]:
optb.information()
optbinning (Version 0.19.0)
Copyright (c) 2019-2024 Guillermo Navas-Palencia, Apache License 2.0
Name : mean texture
Status : OPTIMAL
Pre-binning statistics
Number of bins 8
Solver statistics
Type auto
Number of variables 16
Number of constraints 23
Timing
Total time 0.15 sec
Pre-processing 0.00 sec ( 0.23%)
Estimator 0.01 sec ( 8.47%)
Pre-binning 0.10 sec ( 68.80%)
Solver 0.02 sec ( 15.12%)
Post-processing 0.01 sec ( 6.71%)
Performance: choosing a solver¶
OptimalPWBinning uses the RoPWR library to solving the piecewise regression problem. See https://github.com/guillermo-navas-palencia/ropwr for details.
Robustness: choosing an objective function and regularization¶
OptimalPWBinning uses the RoPWR library to solving the piecewise regression problem. See https://github.com/guillermo-navas-palencia/ropwr for details.
Missing data and special codes¶
For this example, let’s load data from the FICO Explainable Machine Learning Challenge: https://community.fico.com/s/explainable-machine-learning-challenge
[32]:
df = pd.read_csv("data/FICO_challenge/heloc_dataset_v1.csv", sep=",")
The data dictionary of this challenge includes three special values/codes:
-9 No Bureau Record or No Investigation
-8 No Usable/Valid Trades or Inquiries
-7 Condition not Met (e.g. No Inquiries, No Delinquencies)
Version 0.16.0 added support to treat special codes separately.
[33]:
special_codes = {'special_9': -9, 'special_8': -8, 'special_7': -7}
[34]:
variable = "AverageMInFile"
x = df[variable].values
y = df.RiskPerformance.values
[35]:
df.RiskPerformance.unique()
[35]:
array(['Bad', 'Good'], dtype=object)
Target is a categorical dichotomic variable, which can be easily transform into numerical.
[36]:
mask = y == "Bad"
y[mask] = 1
y[~mask] = 0
y = y.astype(int)
[37]:
x[10:20] = -8
x[100:105] = -7
For the sake of completeness, we include a few missing values
[38]:
idx = np.random.randint(0, len(x), 500)
x = x.astype(float)
x[idx] = np.nan
[39]:
optb = OptimalPWBinning(name=variable, special_codes=special_codes, solver="osqp")
optb.fit(x, y, lb=0, ub=1)
[39]:
OptimalPWBinning(estimator=LogisticRegression(), name='AverageMInFile',
solver='osqp',
special_codes={'special_7': -7, 'special_8': -8,
'special_9': -9})
[40]:
optb.information(print_level=1)
optbinning (Version 0.19.0)
Copyright (c) 2019-2024 Guillermo Navas-Palencia, Apache License 2.0
Name : AverageMInFile
Status : OPTIMAL
Pre-binning statistics
Number of bins 12
Solver statistics
Type osqp
Number of variables 24
Number of constraints 39
Timing
Total time 0.31 sec
Pre-processing 0.00 sec ( 0.79%)
Estimator 0.04 sec ( 11.84%)
Pre-binning 0.18 sec ( 59.54%)
Solver 0.04 sec ( 13.81%)
Post-processing 0.04 sec ( 13.44%)
[41]:
binning_table = optb.binning_table
binning_table.build()
[41]:
| Bin | Count | Count (%) | Non-event | Event | c0 | c1 | |
|---|---|---|---|---|---|---|---|
| 0 | (-inf, 30.50) | 543 | 0.051917 | 95 | 448 | 0.794186 | -0.003116 |
| 1 | [30.50, 41.50) | 554 | 0.052969 | 148 | 406 | 0.806671 | -0.003526 |
| 2 | [41.50, 48.50) | 505 | 0.048284 | 144 | 361 | 0.810918 | -0.003628 |
| 3 | [48.50, 54.50) | 527 | 0.050387 | 186 | 341 | 0.816578 | -0.003745 |
| 4 | [54.50, 59.50) | 483 | 0.046180 | 193 | 290 | 0.820645 | -0.003819 |
| 5 | [59.50, 64.50) | 606 | 0.057941 | 261 | 345 | 0.822875 | -0.003857 |
| 6 | [64.50, 69.50) | 642 | 0.061383 | 290 | 352 | 0.830170 | -0.003970 |
| 7 | [69.50, 74.50) | 661 | 0.063199 | 323 | 338 | 0.815715 | -0.003762 |
| 8 | [74.50, 80.50) | 767 | 0.073334 | 403 | 364 | 0.873347 | -0.004536 |
| 9 | [80.50, 97.50) | 1836 | 0.175543 | 1041 | 795 | 0.780597 | -0.003383 |
| 10 | [97.50, 116.50) | 1169 | 0.111770 | 721 | 448 | 1.048544 | -0.006132 |
| 11 | [116.50, inf) | 1098 | 0.104981 | 718 | 380 | 0.480304 | -0.001254 |
| 12 | special_9 | 566 | 0.054116 | 251 | 315 | 0.556537 | 0.000000 |
| 13 | special_8 | 10 | 0.000956 | 2 | 8 | 0.800000 | 0.000000 |
| 14 | special_7 | 5 | 0.000478 | 2 | 3 | 0.600000 | 0.000000 |
| 15 | Missing | 487 | 0.046563 | 222 | 265 | 0.544148 | 0.000000 |
| Totals | 10459 | 1.000000 | 5000 | 5459 | - | - |
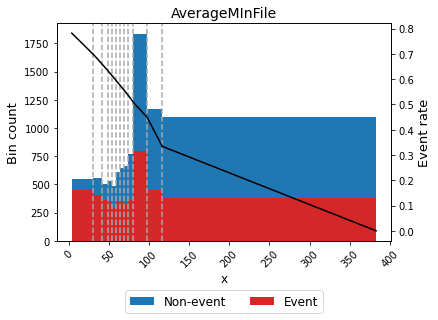
Note the dashed bins 10 and 11, corresponding to the special codes bin and the missing bin, respectively.
[42]:
binning_table.plot(metric="event_rate")
Verbosity option¶
For debugging purposes, we can print information on each step of the computation by triggering the verbose option.
[43]:
optb = OptimalPWBinning(name=variable, solver="osqp", verbose=True)
optb.fit(x, y, lb=0, ub=1)
2024-01-15 00:19:44,441 | INFO : Optimal piecewise binning started.
2024-01-15 00:19:44,444 | INFO : Options: check parameters.
2024-01-15 00:19:44,446 | INFO : Pre-processing started.
2024-01-15 00:19:44,451 | INFO : Pre-processing: number of samples: 10459
2024-01-15 00:19:44,453 | INFO : Pre-processing: number of clean samples: 9972
2024-01-15 00:19:44,454 | INFO : Pre-processing: number of missing samples: 487
2024-01-15 00:19:44,460 | INFO : Pre-processing: number of special samples: 0
2024-01-15 00:19:44,462 | INFO : Pre-processing terminated. Time: 0.0004s
2024-01-15 00:19:44,464 | INFO : Pre-binning: set logistic regression as an estimator.
2024-01-15 00:19:44,467 | INFO : Pre-binning: estimator fitting started.
2024-01-15 00:19:44,536 | INFO : Pre-binning: estimator terminated. Time 0.0719s.
2024-01-15 00:19:44,537 | INFO : Pre-binning: optimal binning started.
2024-01-15 00:19:44,756 | INFO : Pre-binning: number of splits: 9.
2024-01-15 00:19:44,758 | INFO : Pre-binning: no need for subsamples.
2024-01-15 00:19:44,760 | INFO : Pre-binning: optimal binning terminated. Time 0.2209s.
2024-01-15 00:19:44,761 | INFO : Optimizer started.
2024-01-15 00:19:44,767 | INFO : Optimizer: descending monotonic trend.
===============================================================================
CVXPY
v1.2.1
===============================================================================
(CVXPY) Jan 15 12:19:44 AM: Your problem has 20 variables, 4 constraints, and 0 parameters.
(CVXPY) Jan 15 12:19:44 AM: It is compliant with the following grammars: DCP, DQCP
(CVXPY) Jan 15 12:19:44 AM: (If you need to solve this problem multiple times, but with different data, consider using parameters.)
(CVXPY) Jan 15 12:19:44 AM: CVXPY will first compile your problem; then, it will invoke a numerical solver to obtain a solution.
-------------------------------------------------------------------------------
Compilation
-------------------------------------------------------------------------------
(CVXPY) Jan 15 12:19:44 AM: Compiling problem (target solver=OSQP).
(CVXPY) Jan 15 12:19:44 AM: Reduction chain: CvxAttr2Constr -> Qp2SymbolicQp -> QpMatrixStuffing -> OSQP
(CVXPY) Jan 15 12:19:44 AM: Applying reduction CvxAttr2Constr
(CVXPY) Jan 15 12:19:44 AM: Applying reduction Qp2SymbolicQp
(CVXPY) Jan 15 12:19:44 AM: Applying reduction QpMatrixStuffing
(CVXPY) Jan 15 12:19:44 AM: Applying reduction OSQP
(CVXPY) Jan 15 12:19:44 AM: Finished problem compilation (took 6.110e-02 seconds).
-------------------------------------------------------------------------------
Numerical solver
-------------------------------------------------------------------------------
(CVXPY) Jan 15 12:19:44 AM: Invoking solver OSQP to obtain a solution.
-----------------------------------------------------------------
OSQP v0.6.0 - Operator Splitting QP Solver
(c) Bartolomeo Stellato, Goran Banjac
University of Oxford - Stanford University 2019
-----------------------------------------------------------------
problem: variables n = 20, constraints m = 33
nnz(P) + nnz(A) = 84
settings: linear system solver = qdldl,
eps_abs = 1.0e-05, eps_rel = 1.0e-05,
eps_prim_inf = 1.0e-04, eps_dual_inf = 1.0e-04,
rho = 1.00e-01 (adaptive),
sigma = 1.00e-06, alpha = 1.60, max_iter = 10000
check_termination: on (interval 25),
scaling: on, scaled_termination: off
warm start: on, polish: on, time_limit: off
iter objective pri res dua res rho time
1 -1.9687e+03 7.88e-03 9.98e+04 1.00e-01 9.84e-04s
75 -2.8189e+03 2.91e-06 1.15e+00 1.00e-01 4.15e-03s
plsh -2.8189e+03 1.82e-16 5.12e-11 -------- 7.45e-03s
status: solved
solution polish: successful
number of iterations: 75
optimal objective: -2818.8684
run time: 7.45e-03s
optimal rho estimate: 2.44e-02
-------------------------------------------------------------------------------
Summary
-------------------------------------------------------------------------------
(CVXPY) Jan 15 12:19:44 AM: Problem status: optimal
(CVXPY) Jan 15 12:19:44 AM: Optimal value: -2.819e+03
(CVXPY) Jan 15 12:19:44 AM: Compilation took 6.110e-02 seconds
(CVXPY) Jan 15 12:19:44 AM: Solver (including time spent in interface) took 1.754e-02 seconds
2024-01-15 00:19:44,911 | INFO : Optimizer terminated. Time: 0.1424s
2024-01-15 00:19:44,913 | INFO : Post-processing started.
2024-01-15 00:19:44,914 | INFO : Post-processing: compute binning information.
2024-01-15 00:19:44,924 | INFO : Post-processing: compute performance metrics.
2024-01-15 00:19:44,962 | INFO : Post-processing terminated. Time: 0.0455s
2024-01-15 00:19:44,965 | INFO : Optimal piecewise binning terminated. Status: OPTIMAL. Time: 0.5233s
[43]:
OptimalPWBinning(estimator=LogisticRegression(), name='AverageMInFile',
solver='osqp', verbose=True)