Tutorial: optimal binning 2D with binary target¶
As usual, let’s load a well-known dataset from the UCI repository and transform the data into a pandas.DataFrame.
[1]:
import numpy as np
import pandas as pd
from sklearn.datasets import load_breast_cancer
[2]:
data = load_breast_cancer()
df = pd.DataFrame(data.data, columns=data.feature_names)
We choose two variables to discretize and the binary target.
[3]:
variable1 = "mean radius"
variable2 = "worst concavity"
x = df[variable1].values
y = df[variable2].values
z = data.target
Import and instantiate an OptimalBinning2D object class. We pass the variable names (coordinates x and y), and a solver, in this case, we choose the constraint programming solver.
[4]:
from optbinning import OptimalBinning2D
[5]:
optb = OptimalBinning2D(name_x=variable1, name_y=variable2, solver="cp")
We fit the optimal binning object with arrays x, y, and z.
[6]:
optb.fit(x, y, z)
[6]:
OptimalBinning2D(name_x='mean radius', name_y='worst concavity')
Similar to other OptBinning classes, you can inspect the attributes status and splits. In this case, the splits shown are actually the bins, but the splits name is used to maintain API homogeneity.
[7]:
optb.status
[7]:
'OPTIMAL'
[8]:
optb.splits
[8]:
([[-inf, 13.704999923706055],
[13.704999923706055, 15.045000076293945],
[15.045000076293945, 16.925000190734863],
[16.925000190734863, inf],
[-inf, 13.09499979019165],
[13.09499979019165, 13.704999923706055],
[15.045000076293945, 16.925000190734863],
[13.09499979019165, 13.704999923706055],
[13.704999923706055, 15.045000076293945],
[15.045000076293945, 16.925000190734863],
[13.09499979019165, 13.704999923706055],
[13.704999923706055, 15.045000076293945],
[15.045000076293945, inf],
[-inf, 13.09499979019165],
[13.09499979019165, 13.704999923706055],
[13.704999923706055, 15.045000076293945]],
[[-inf, 0.20795000344514847],
[-inf, 0.2604999989271164],
[-inf, 0.20795000344514847],
[-inf, 0.31530000269412994],
[0.20795000344514847, 0.37815000116825104],
[0.20795000344514847, 0.2604999989271164],
[0.20795000344514847, 0.2604999989271164],
[0.2604999989271164, 0.31530000269412994],
[0.2604999989271164, 0.31530000269412994],
[0.2604999989271164, 0.31530000269412994],
[0.31530000269412994, 0.37815000116825104],
[0.31530000269412994, 0.37815000116825104],
[0.31530000269412994, inf],
[0.37815000116825104, inf],
[0.37815000116825104, inf],
[0.37815000116825104, inf]])
The binning table¶
The binning table follows the same structure as the unidimensional binning, except for having two Bin columns, one for each variable (coordinate). The option show_bin_xy=True in method build combines both columns to obtain a single Bin column.
[9]:
optb.binning_table.build()
[9]:
| Bin x | Bin y | Count | Count (%) | Non-event | Event | Event rate | WoE | IV | JS | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | (-inf, 13.70) | (-inf, 0.21) | 219 | 0.384886 | 1 | 218 | 0.995434 | -4.863346 | 2.946834 | 0.199430 |
| 1 | [13.70, 15.05) | (-inf, 0.26) | 45 | 0.079086 | 1 | 44 | 0.977778 | -3.263040 | 0.386776 | 0.034251 |
| 2 | [15.05, 16.93) | (-inf, 0.21) | 8 | 0.014060 | 2 | 6 | 0.750000 | -0.577463 | 0.004257 | 0.000525 |
| 3 | [16.93, inf) | (-inf, 0.32) | 21 | 0.036907 | 20 | 1 | 0.047619 | 3.516882 | 0.321930 | 0.027320 |
| 4 | (-inf, 13.09) | [0.21, 0.38) | 48 | 0.084359 | 1 | 47 | 0.979167 | -3.328998 | 0.422569 | 0.037010 |
| 5 | [13.09, 13.70) | [0.21, 0.26) | 6 | 0.010545 | 1 | 5 | 0.833333 | -1.088288 | 0.010109 | 0.001205 |
| 6 | [15.05, 16.93) | [0.21, 0.26) | 6 | 0.010545 | 4 | 2 | 0.333333 | 1.214297 | 0.016108 | 0.001898 |
| 7 | [13.09, 13.70) | [0.26, 0.32) | 4 | 0.007030 | 1 | 3 | 0.750000 | -0.577463 | 0.002129 | 0.000262 |
| 8 | [13.70, 15.05) | [0.26, 0.32) | 9 | 0.015817 | 5 | 4 | 0.444444 | 0.744293 | 0.009215 | 0.001126 |
| 9 | [15.05, 16.93) | [0.26, 0.32) | 8 | 0.014060 | 7 | 1 | 0.125000 | 2.467060 | 0.074549 | 0.007501 |
| 10 | [13.09, 13.70) | [0.32, 0.38) | 7 | 0.012302 | 3 | 4 | 0.571429 | 0.233467 | 0.000688 | 0.000086 |
| 11 | [13.70, 15.05) | [0.32, 0.38) | 12 | 0.021090 | 7 | 5 | 0.416667 | 0.857622 | 0.016306 | 0.001978 |
| 12 | [15.05, inf) | [0.32, inf) | 129 | 0.226714 | 128 | 1 | 0.007752 | 5.373180 | 3.229133 | 0.201294 |
| 13 | (-inf, 13.09) | [0.38, inf) | 22 | 0.038664 | 11 | 11 | 0.500000 | 0.521150 | 0.010983 | 0.001358 |
| 14 | [13.09, 13.70) | [0.38, inf) | 8 | 0.014060 | 5 | 3 | 0.375000 | 1.031975 | 0.015667 | 0.001876 |
| 15 | [13.70, 15.05) | [0.38, inf) | 17 | 0.029877 | 15 | 2 | 0.117647 | 2.536053 | 0.165230 | 0.016450 |
| 16 | Special | Special | 0 | 0.000000 | 0 | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 17 | Missing | Missing | 0 | 0.000000 | 0 | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| Totals | 569 | 1.000000 | 212 | 357 | 0.627417 | 7.632482 | 0.533569 |
[10]:
optb.binning_table.build(show_bin_xy=True)
[10]:
| Bin | Count | Count (%) | Non-event | Event | Event rate | WoE | IV | JS | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | (-inf, 13.70) $\cup$ (-inf, 0.21) | 219 | 0.384886 | 1 | 218 | 0.995434 | -4.863346 | 2.946834 | 0.199430 |
| 1 | [13.70, 15.05) $\cup$ (-inf, 0.26) | 45 | 0.079086 | 1 | 44 | 0.977778 | -3.263040 | 0.386776 | 0.034251 |
| 2 | [15.05, 16.93) $\cup$ (-inf, 0.21) | 8 | 0.014060 | 2 | 6 | 0.750000 | -0.577463 | 0.004257 | 0.000525 |
| 3 | [16.93, inf) $\cup$ (-inf, 0.32) | 21 | 0.036907 | 20 | 1 | 0.047619 | 3.516882 | 0.321930 | 0.027320 |
| 4 | (-inf, 13.09) $\cup$ [0.21, 0.38) | 48 | 0.084359 | 1 | 47 | 0.979167 | -3.328998 | 0.422569 | 0.037010 |
| 5 | [13.09, 13.70) $\cup$ [0.21, 0.26) | 6 | 0.010545 | 1 | 5 | 0.833333 | -1.088288 | 0.010109 | 0.001205 |
| 6 | [15.05, 16.93) $\cup$ [0.21, 0.26) | 6 | 0.010545 | 4 | 2 | 0.333333 | 1.214297 | 0.016108 | 0.001898 |
| 7 | [13.09, 13.70) $\cup$ [0.26, 0.32) | 4 | 0.007030 | 1 | 3 | 0.750000 | -0.577463 | 0.002129 | 0.000262 |
| 8 | [13.70, 15.05) $\cup$ [0.26, 0.32) | 9 | 0.015817 | 5 | 4 | 0.444444 | 0.744293 | 0.009215 | 0.001126 |
| 9 | [15.05, 16.93) $\cup$ [0.26, 0.32) | 8 | 0.014060 | 7 | 1 | 0.125000 | 2.467060 | 0.074549 | 0.007501 |
| 10 | [13.09, 13.70) $\cup$ [0.32, 0.38) | 7 | 0.012302 | 3 | 4 | 0.571429 | 0.233467 | 0.000688 | 0.000086 |
| 11 | [13.70, 15.05) $\cup$ [0.32, 0.38) | 12 | 0.021090 | 7 | 5 | 0.416667 | 0.857622 | 0.016306 | 0.001978 |
| 12 | [15.05, inf) $\cup$ [0.32, inf) | 129 | 0.226714 | 128 | 1 | 0.007752 | 5.373180 | 3.229133 | 0.201294 |
| 13 | (-inf, 13.09) $\cup$ [0.38, inf) | 22 | 0.038664 | 11 | 11 | 0.500000 | 0.521150 | 0.010983 | 0.001358 |
| 14 | [13.09, 13.70) $\cup$ [0.38, inf) | 8 | 0.014060 | 5 | 3 | 0.375000 | 1.031975 | 0.015667 | 0.001876 |
| 15 | [13.70, 15.05) $\cup$ [0.38, inf) | 17 | 0.029877 | 15 | 2 | 0.117647 | 2.536053 | 0.165230 | 0.016450 |
| 16 | Special | 0 | 0.000000 | 0 | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 17 | Missing | 0 | 0.000000 | 0 | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| Totals | 569 | 1.000000 | 212 | 357 | 0.627417 | 7.632482 | 0.533569 |
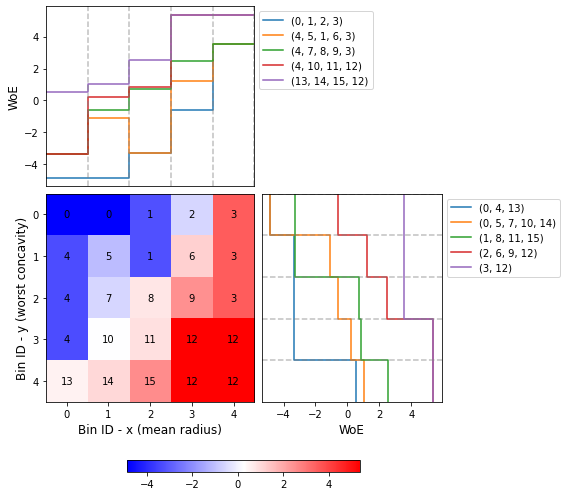
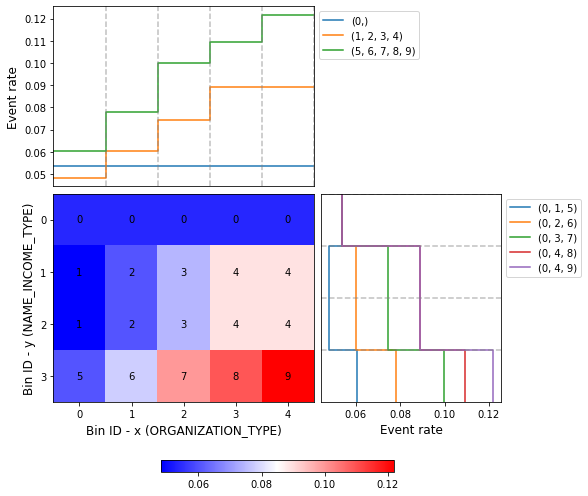
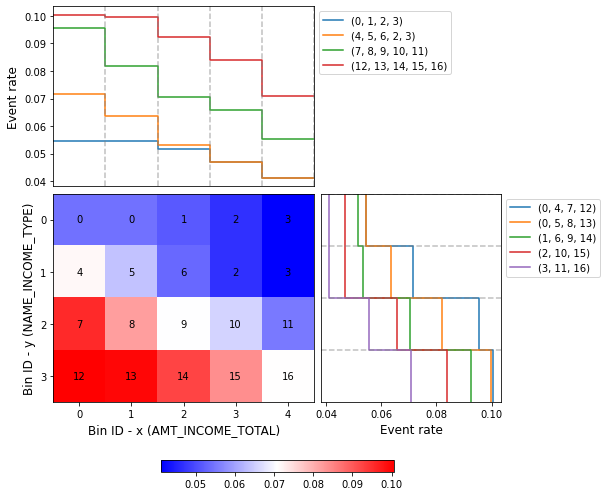
You can use the method plot to visualize the histogram 2D and WoE or event rate curve. Note that the Bin ID corresponds to the binning table index. These are the key points to correctly interpret the plots belows:
Bins can only be rectangles. If a bin is composed by \(m\) squares, the Bin ID is shown \(m\) times.
The upper left plot shows the WoE/event rate on the x-axis; the bin paths left-right.
The lower right plot shows the WoE/event rate on the y-axis; the bin paths top-down.
[11]:
optb.binning_table.plot(metric="woe")
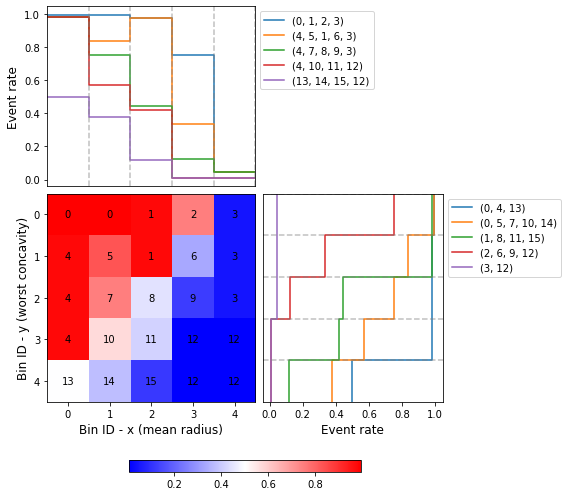
[12]:
optb.binning_table.plot(metric="event_rate")
Event rate / WoE transformation¶
Now that we have checked the binned data, we can transform our original data into WoE or event rate values. You can check the correctness of the transformation using pandas value_counts method, for instance. Note that both x and y are required, and a single array is returned with the transformation.
[13]:
z_transform_woe = optb.transform(x, y, metric="woe")
pd.Series(z_transform_woe).value_counts()
[13]:
-4.863346 219
5.373180 129
-3.328998 48
-3.263040 45
0.521150 22
3.516882 21
2.536053 17
0.857622 12
-0.577463 12
0.744293 9
2.467060 8
1.031975 8
0.233467 7
-1.088288 6
1.214297 6
dtype: int64
[14]:
z_transform_event_rate = optb.transform(x, y, metric="event_rate")
pd.Series(z_transform_event_rate).value_counts()
[14]:
0.995434 219
0.007752 129
0.979167 48
0.977778 45
0.500000 22
0.047619 21
0.117647 17
0.416667 12
0.750000 12
0.444444 9
0.125000 8
0.375000 8
0.571429 7
0.833333 6
0.333333 6
dtype: int64
[15]:
z_transform_indices = optb.transform(x, y, metric="indices")
pd.Series(z_transform_indices).value_counts()
[15]:
0 219
12 129
4 48
1 45
13 22
3 21
15 17
11 12
8 9
2 8
9 8
14 8
10 7
5 6
6 6
7 4
dtype: int64
If metric="bins" the bin ids are combined.
[16]:
z_transform_bins = optb.transform(x, y, metric="bins")
[17]:
pd.Series(z_transform_bins).value_counts()
[17]:
(-inf, 13.70) $\cup$ (-inf, 0.21) 219
[15.05, inf) $\cup$ [0.32, inf) 129
(-inf, 13.09) $\cup$ [0.21, 0.38) 48
[13.70, 15.05) $\cup$ (-inf, 0.26) 45
(-inf, 13.09) $\cup$ [0.38, inf) 22
[16.93, inf) $\cup$ (-inf, 0.32) 21
[13.70, 15.05) $\cup$ [0.38, inf) 17
[13.70, 15.05) $\cup$ [0.32, 0.38) 12
[13.70, 15.05) $\cup$ [0.26, 0.32) 9
[15.05, 16.93) $\cup$ [0.26, 0.32) 8
[13.09, 13.70) $\cup$ [0.38, inf) 8
[15.05, 16.93) $\cup$ (-inf, 0.21) 8
[13.09, 13.70) $\cup$ [0.32, 0.38) 7
[15.05, 16.93) $\cup$ [0.21, 0.26) 6
[13.09, 13.70) $\cup$ [0.21, 0.26) 6
[13.09, 13.70) $\cup$ [0.26, 0.32) 4
dtype: int64
Binning table statistical analysis¶
The analysis method performs a statistical analysis of the binning table, computing the statistics Gini index, Information Value (IV), Jensen-Shannon divergence, and the quality score. The report is the same that the one for unidimensional binning with a binary target. The main difference is that the significant tests for each bin are performed with respect to all its linked bins.
[18]:
optb.binning_table.analysis()
------------------------------------------------
OptimalBinning: Binary Binning Table 2D Analysis
------------------------------------------------
General metrics
Gini index 0.96381005
IV (Jeffrey) 7.63248244
JS (Jensen-Shannon) 0.53356918
Hellinger 0.66868014
Triangular 1.62726969
KS 0.77651815
HHI 0.21836787
HHI (normalized) 0.17238951
Cramer's V 0.89619441
Quality score 0.00000000
Significance tests
Bin A Bin B t-statistic p-value P[A > B] P[B > A]
0 1 1.547799 2.134607e-01 0.832082 1.679183e-01
0 4 1.401336 2.365000e-01 0.822661 1.773392e-01
0 5 17.418530 2.998882e-05 0.977759 2.224079e-02
1 2 6.599481 1.020085e-02 0.983958 1.604164e-02
1 6 24.864348 6.150953e-07 0.999999 1.269024e-06
1 8 21.600000 3.358518e-06 0.999997 3.065628e-06
2 3 15.607452 7.794679e-05 0.999984 1.596851e-05
2 6 2.430556 1.189907e-01 0.954856 4.514395e-02
3 12 2.181916 1.396405e-01 0.865053 1.349470e-01
4 5 3.180288 7.453157e-02 0.903885 9.611469e-02
4 7 5.243333 2.203102e-02 0.940065 5.993476e-02
4 10 15.060326 1.041290e-04 0.999472 5.281334e-04
4 13 24.385177 7.887324e-07 1.000000 2.478198e-08
5 1 2.931633 8.685961e-02 0.101859 8.981415e-01
5 7 0.104167 7.468856e-01 0.625007 3.749931e-01
6 3 3.857143 4.953461e-02 0.966923 3.307725e-02
6 9 0.883838 3.471525e-01 0.848618 1.513821e-01
7 8 1.040344 3.077415e-01 0.878999 1.210008e-01
7 10 0.350765 5.536802e-01 0.762036 2.379644e-01
8 9 2.081713 1.490728e-01 0.948990 5.101023e-02
8 11 0.016204 8.987079e-01 0.550579 4.494212e-01
9 3 0.540234 4.623359e-01 0.740855 2.591449e-01
9 12 7.198597 7.296061e-03 0.948279 5.172121e-02
10 11 0.424735 5.145836e-01 0.753507 2.464934e-01
10 14 0.578763 4.467977e-01 0.791467 2.085325e-01
11 12 45.057860 1.912979e-11 0.999999 8.195706e-07
11 15 3.434842 6.383469e-02 0.973833 2.616650e-02
13 14 0.368304 5.439304e-01 0.741788 2.582125e-01
14 15 2.251838 1.334558e-01 0.933081 6.691866e-02
15 12 9.013449 2.680002e-03 0.988496 1.150434e-02
The OptimalBinning2D can print overview information about the options settings, problem statistics, and the solution of the computation. Use print_level=2, to include the list of all options.
[19]:
optb.information(print_level=2)
optbinning (Version 0.19.0)
Copyright (c) 2019-2024 Guillermo Navas-Palencia, Apache License 2.0
Begin options
name_x mean radius * U
name_y worst concavity * U
dtype_x numerical * d
dtype_y numerical * d
prebinning_method cart * d
strategy grid * d
solver cp * d
divergence iv * d
max_n_prebins_x 5 * d
max_n_prebins_y 5 * d
min_prebin_size_x 0.05 * d
min_prebin_size_y 0.05 * d
min_n_bins no * d
max_n_bins no * d
min_bin_size no * d
max_bin_size no * d
min_bin_n_nonevent no * d
max_bin_n_nonevent no * d
min_bin_n_event no * d
max_bin_n_event no * d
monotonic_trend_x no * d
monotonic_trend_y no * d
min_event_rate_diff_x 0 * d
min_event_rate_diff_y 0 * d
gamma 0 * d
special_codes_x no * d
special_codes_y no * d
split_digits no * d
n_jobs 1 * d
time_limit 100 * d
verbose False * d
End options
Name : mean radius-worst concavity
Status : OPTIMAL
Pre-binning statistics
Number of pre-bins 25
Number of refinements 17
Solver statistics
Type cp
Number of booleans 10
Number of branches 24
Number of conflicts 0
Objective value 7632473
Best objective bound 7632473
Timing
Total time 0.06 sec
Pre-processing 0.00 sec ( 0.55%)
Pre-binning 0.00 sec ( 4.77%)
Solver 0.05 sec ( 90.56%)
model generation 0.05 sec ( 84.84%)
optimizer 0.01 sec ( 15.16%)
Post-processing 0.00 sec ( 3.21%)
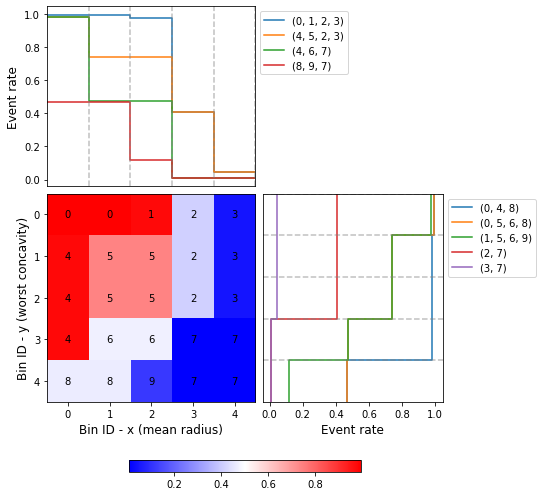
Event rate / WoE monotonicity¶
The monotonic_trend_x and monotonic_trend_y options permit forcing a monotonic trend to the event rate curve on each axis. By default, both options are set to None. There are two options available: “ascending” and “descending”. In this example, we force both trends to be “descending”, and a minimum bin size of 0.025 (2.5%).
[20]:
optb = OptimalBinning2D(name_x=variable1, name_y=variable2, monotonic_trend_x="descending",
monotonic_trend_y="descending", min_bin_size=0.025)
optb.fit(x, y, z)
[20]:
OptimalBinning2D(min_bin_size=0.025, monotonic_trend_x='descending',
monotonic_trend_y='descending', name_x='mean radius',
name_y='worst concavity')
[21]:
optb.binning_table.build()
[21]:
| Bin x | Bin y | Count | Count (%) | Non-event | Event | Event rate | WoE | IV | JS | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | (-inf, 13.70) | (-inf, 0.21) | 219 | 0.384886 | 1 | 218 | 0.995434 | -4.863346 | 2.946834 | 0.199430 |
| 1 | [13.70, 15.05) | (-inf, 0.21) | 37 | 0.065026 | 1 | 36 | 0.972973 | -3.062369 | 0.294365 | 0.026948 |
| 2 | [15.05, 16.93) | (-inf, 0.32) | 22 | 0.038664 | 13 | 9 | 0.409091 | 0.888874 | 0.032098 | 0.003885 |
| 3 | [16.93, inf) | (-inf, 0.32) | 21 | 0.036907 | 20 | 1 | 0.047619 | 3.516882 | 0.321930 | 0.027320 |
| 4 | (-inf, 13.09) | [0.21, 0.38) | 48 | 0.084359 | 1 | 47 | 0.979167 | -3.328998 | 0.422569 | 0.037010 |
| 5 | [13.09, 15.05) | [0.21, 0.32) | 27 | 0.047452 | 7 | 20 | 0.740741 | -0.528673 | 0.012161 | 0.001503 |
| 6 | [13.09, 15.05) | [0.32, 0.38) | 19 | 0.033392 | 10 | 9 | 0.473684 | 0.626510 | 0.013758 | 0.001692 |
| 7 | [15.05, inf) | [0.32, inf) | 129 | 0.226714 | 128 | 1 | 0.007752 | 5.373180 | 3.229133 | 0.201294 |
| 8 | (-inf, 13.70) | [0.38, inf) | 30 | 0.052724 | 16 | 14 | 0.466667 | 0.654681 | 0.023736 | 0.002915 |
| 9 | [13.70, 15.05) | [0.38, inf) | 17 | 0.029877 | 15 | 2 | 0.117647 | 2.536053 | 0.165230 | 0.016450 |
| 10 | Special | Special | 0 | 0.000000 | 0 | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 11 | Missing | Missing | 0 | 0.000000 | 0 | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| Totals | 569 | 1.000000 | 212 | 357 | 0.627417 | 7.461814 | 0.518447 |
[22]:
optb.binning_table.plot(metric="event_rate")
[23]:
optb.binning_table.analysis()
------------------------------------------------
OptimalBinning: Binary Binning Table 2D Analysis
------------------------------------------------
General metrics
Gini index 0.95655621
IV (Jeffrey) 7.46181417
JS (Jensen-Shannon) 0.51844733
Hellinger 0.65109672
Triangular 1.57873476
KS 0.72434068
HHI 0.22077705
HHI (normalized) 0.14993861
Cramer's V 0.88274577
Quality score 0.00000000
Significance tests
Bin A Bin B t-statistic p-value P[A > B] P[B > A]
0 1 2.060028 1.512074e-01 0.858293 1.417071e-01
0 4 1.401336 2.365000e-01 0.822661 1.773392e-01
0 5 49.557596 1.926326e-12 1.000000 3.782008e-11
1 2 24.238873 8.509727e-07 1.000000 9.439925e-09
1 5 7.696840 5.531760e-03 0.998790 1.209527e-03
2 3 7.865847 5.037723e-03 0.999413 5.874914e-04
2 7 48.954531 2.619654e-12 1.000000 6.888954e-10
3 7 2.181916 1.396405e-01 0.865053 1.349470e-01
4 5 10.308808 1.323968e-03 0.999676 3.238203e-04
4 6 25.345514 4.792657e-07 1.000000 1.762382e-08
4 8 28.448939 9.620246e-08 1.000000 4.164320e-10
5 2 5.519682 1.880367e-02 0.992461 7.538668e-03
5 6 3.413773 6.465445e-02 0.970465 2.953487e-02
6 7 57.065224 4.215951e-14 1.000000 1.266293e-10
6 8 0.002300 9.617489e-01 0.518436 4.815645e-01
6 9 5.359977 2.060404e-02 0.994187 5.812630e-03
8 9 5.886891 1.525401e-02 0.996741 3.258617e-03
9 7 9.013449 2.680002e-03 0.988496 1.150434e-02
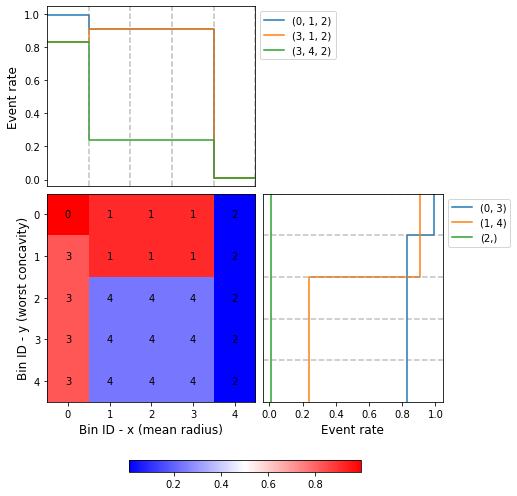
Reduction of dominating bins¶
To produce more homogeneous bins, the formulation includes a constraint to reduce the difference between the largest and smallest bin. The added regularization parameter gamma controls the importance of the reduction term. Larger values specify stronger regularization.
[24]:
optb = OptimalBinning2D(name_x=variable1, name_y=variable2, gamma=600)
optb.fit(x, y, z)
[24]:
OptimalBinning2D(gamma=600, name_x='mean radius', name_y='worst concavity')
[25]:
optb.binning_table.build()
[25]:
| Bin x | Bin y | Count | Count (%) | Non-event | Event | Event rate | WoE | IV | JS | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | (-inf, 13.09) | (-inf, 0.21) | 195 | 0.342707 | 1 | 194 | 0.994872 | -4.746709 | 2.557054 | 0.176405 |
| 1 | [13.09, 16.93) | (-inf, 0.26) | 89 | 0.156415 | 8 | 81 | 0.910112 | -1.793858 | 0.339317 | 0.037510 |
| 2 | [16.93, inf) | (-inf, inf) | 118 | 0.207381 | 117 | 1 | 0.008475 | 5.283323 | 2.900997 | 0.183436 |
| 3 | (-inf, 13.09) | [0.21, inf) | 70 | 0.123023 | 12 | 58 | 0.828571 | -1.054387 | 0.111619 | 0.013340 |
| 4 | [13.09, 16.93) | [0.26, inf) | 97 | 0.170475 | 74 | 23 | 0.237113 | 1.689720 | 0.480947 | 0.053853 |
| 5 | Special | Special | 0 | 0.000000 | 0 | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 6 | Missing | Missing | 0 | 0.000000 | 0 | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| Totals | 569 | 1.000000 | 212 | 357 | 0.627417 | 6.389933 | 0.464545 |
[26]:
optb.binning_table.plot(metric="event_rate")
Missing data and special codes¶
For this example, let’s load data from the FICO Explainable Machine Learning Challenge: https://community.fico.com/s/explainable-machine-learning-challenge
[27]:
df = pd.read_csv("data/FICO_challenge/heloc_dataset_v1.csv", sep=",")
The data dictionary of this challenge includes three special values/codes:
-9 No Bureau Record or No Investigation
-8 No Usable/Valid Trades or Inquiries
-7 Condition not Met (e.g. No Inquiries, No Delinquencies)
All three special codes are considered for both variables.
[28]:
special_codes_x = [-9, -8, -7]
special_codes_y = [-9, -8, -7]
[29]:
variable1 = "AverageMInFile"
variable2 = "MSinceOldestTradeOpen"
x = df[variable1].values
y = df[variable2].values
z = df.RiskPerformance.values
mask = z == "Bad"
z[mask] = 1
z[~mask] = 0
z = z.astype(int)
For the sake of completeness, we include a few missing values
[30]:
idx = np.random.randint(0, len(x), 500)
x = x.astype(float)
x[idx] = np.nan
[31]:
optb = OptimalBinning2D(name_x=variable1, name_y=variable2,
monotonic_trend_y="ascending",
special_codes_x=special_codes_x,
special_codes_y=special_codes_y)
optb.fit(x, y, z)
[31]:
OptimalBinning2D(monotonic_trend_y='ascending', name_x='AverageMInFile',
name_y='MSinceOldestTradeOpen', special_codes_x=[-9, -8, -7],
special_codes_y=[-9, -8, -7])
[32]:
optb.binning_table.build()
[32]:
| Bin x | Bin y | Count | Count (%) | Non-event | Event | Event rate | WoE | IV | JS | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | (-inf, 48.50) | (-inf, inf) | 1556 | 0.148289 | 374 | 1182 | 0.759640 | -1.063165 | 0.150230 | 0.017941 |
| 1 | [48.50, 64.50) | (-inf, 184.50) | 1215 | 0.115791 | 480 | 735 | 0.604938 | -0.338542 | 0.013050 | 0.001623 |
| 2 | [64.50, 81.50) | (-inf, inf) | 2193 | 0.208996 | 1086 | 1107 | 0.504788 | 0.068390 | 0.000979 | 0.000122 |
| 3 | [81.50, 101.50) | (-inf, inf) | 1957 | 0.186505 | 1118 | 839 | 0.428717 | 0.374629 | 0.026085 | 0.003242 |
| 4 | [101.50, inf) | (-inf, inf) | 1898 | 0.180882 | 1205 | 693 | 0.365121 | 0.640748 | 0.072809 | 0.008949 |
| 5 | [48.50, 64.50) | [184.50, inf) | 360 | 0.034309 | 140 | 220 | 0.611111 | -0.364442 | 0.004472 | 0.000556 |
| 6 | Special | Special | 827 | 0.078814 | 375 | 452 | 0.546554 | -0.099213 | 0.000773 | 0.000097 |
| 7 | Missing | Missing | 487 | 0.046412 | 239 | 248 | 0.509240 | 0.050578 | 0.000119 | 0.000015 |
| Totals | 10493 | 1.000000 | 5017 | 5476 | 0.521872 | 0.268516 | 0.032545 |
[33]:
optb.binning_table.plot(metric="event_rate")
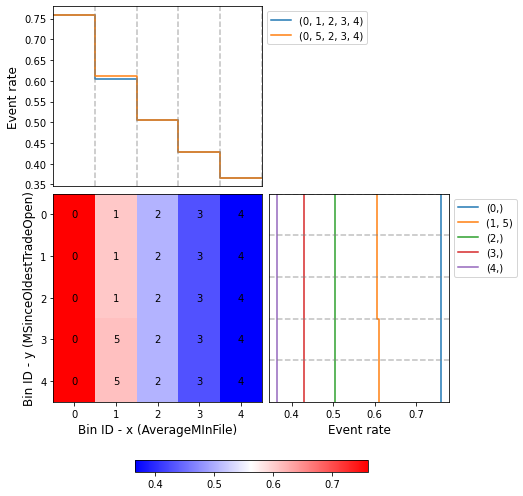
Note that the special and missing bins are not included in the plot above.
Strategy CART (Experimental)¶
In this last section, provide guidance to handle large grids. These large grids are generated when the parameters max_n_prebins_* increase (the default value is set to 5). The performance of the optimization solvers CP and MIP is instance dependent. Based on experiments, the CP solver tends to perform better on very large grids, but on small and medium sizes the MIP can be often faster.
10 prebins (100 grid elements)¶
[34]:
variable1 = "ExternalRiskEstimate"
variable2 = "AverageMInFile"
x = df[variable1].values
y = df[variable2].values
[35]:
optb = OptimalBinning2D(name_x=variable1, name_y=variable2,
solver="cp",
monotonic_trend_x="descending",
monotonic_trend_y="descending",
max_n_prebins_x=10, max_n_prebins_y=10,
min_bin_size=0.05,
special_codes_x=special_codes_x,
special_codes_y=special_codes_y)
optb.fit(x, y, z)
[35]:
OptimalBinning2D(max_n_prebins_x=10, max_n_prebins_y=10, min_bin_size=0.05,
monotonic_trend_x='descending', monotonic_trend_y='descending',
name_x='ExternalRiskEstimate', name_y='AverageMInFile',
special_codes_x=[-9, -8, -7], special_codes_y=[-9, -8, -7])
[36]:
optb.binning_table.build()
[36]:
| Bin x | Bin y | Count | Count (%) | Non-event | Event | Event rate | WoE | IV | JS | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | (-inf, 63.50) | (-inf, 54.50) | 749 | 0.071613 | 87 | 662 | 0.883845 | -1.941530 | 0.201662 | 0.021871 |
| 1 | [63.50, 70.50) | (-inf, 54.50) | 765 | 0.073143 | 187 | 578 | 0.755556 | -1.040638 | 0.071263 | 0.008527 |
| 2 | [70.50, 78.50) | (-inf, 64.50) | 815 | 0.077923 | 343 | 472 | 0.579141 | -0.231421 | 0.004134 | 0.000516 |
| 3 | [78.50, 80.50) | (-inf, inf) | 588 | 0.056220 | 405 | 183 | 0.311224 | 0.882229 | 0.041886 | 0.005072 |
| 4 | [80.50, inf) | (-inf, 74.50) | 563 | 0.053829 | 405 | 158 | 0.280639 | 1.029120 | 0.053573 | 0.006416 |
| 5 | (-inf, 59.50) | [54.50, inf) | 746 | 0.071326 | 131 | 615 | 0.824397 | -1.458597 | 0.126107 | 0.014500 |
| 6 | [59.50, 67.50) | [54.50, 81.50) | 828 | 0.079166 | 213 | 615 | 0.742754 | -0.972502 | 0.068132 | 0.008196 |
| 7 | [67.50, 70.50) | [54.50, inf) | 735 | 0.070274 | 309 | 426 | 0.579592 | -0.233270 | 0.003787 | 0.000472 |
| 8 | [70.50, 75.50) | [64.50, inf) | 1049 | 0.100296 | 596 | 453 | 0.431840 | 0.362176 | 0.013117 | 0.001631 |
| 9 | [75.50, 78.50) | [64.50, inf) | 549 | 0.052491 | 372 | 177 | 0.322404 | 0.830572 | 0.034864 | 0.004237 |
| 10 | [80.50, 84.50) | [74.50, inf) | 668 | 0.063868 | 528 | 140 | 0.209581 | 1.415282 | 0.113158 | 0.013071 |
| 11 | [84.50, inf) | [74.50, inf) | 1080 | 0.103260 | 917 | 163 | 0.150926 | 1.815185 | 0.278705 | 0.030726 |
| 12 | [59.50, 67.50) | [81.50, inf) | 726 | 0.069414 | 240 | 486 | 0.669421 | -0.617742 | 0.025344 | 0.003119 |
| 13 | Special | Special | 598 | 0.057176 | 267 | 331 | 0.553512 | -0.127042 | 0.000919 | 0.000115 |
| 14 | Missing | Missing | 0 | 0.000000 | 0 | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| Totals | 10459 | 1.000000 | 5000 | 5459 | 0.521943 | 1.036652 | 0.118468 |
[37]:
optb.binning_table.plot(metric="event_rate")
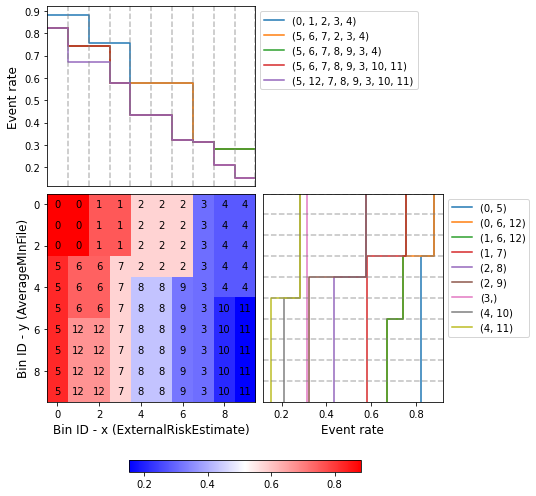
[38]:
optb.information(print_level=1)
optbinning (Version 0.19.0)
Copyright (c) 2019-2024 Guillermo Navas-Palencia, Apache License 2.0
Name : ExternalRiskEstimate-AverageMInFile
Status : OPTIMAL
Pre-binning statistics
Number of pre-bins 100
Number of refinements 844
Solver statistics
Type cp
Number of booleans 2154
Number of branches 19433
Number of conflicts 8439
Objective value 1098271
Best objective bound 1098271
Timing
Total time 11.72 sec
Pre-processing 0.00 sec ( 0.04%)
Pre-binning 0.02 sec ( 0.14%)
Solver 11.69 sec ( 99.75%)
model generation 2.96 sec ( 25.30%)
optimizer 8.73 sec ( 74.70%)
Post-processing 0.00 sec ( 0.02%)
[39]:
optb = OptimalBinning2D(name_x=variable1, name_y=variable2,
solver="mip",
monotonic_trend_x="descending",
monotonic_trend_y="descending",
max_n_prebins_x=10, max_n_prebins_y=10,
min_bin_size=0.05,
special_codes_x=special_codes_x,
special_codes_y=special_codes_y)
optb.fit(x, y, z)
[39]:
OptimalBinning2D(max_n_prebins_x=10, max_n_prebins_y=10, min_bin_size=0.05,
monotonic_trend_x='descending', monotonic_trend_y='descending',
name_x='ExternalRiskEstimate', name_y='AverageMInFile',
solver='mip', special_codes_x=[-9, -8, -7],
special_codes_y=[-9, -8, -7])
[40]:
optb.information(print_level=1)
optbinning (Version 0.19.0)
Copyright (c) 2019-2024 Guillermo Navas-Palencia, Apache License 2.0
Name : ExternalRiskEstimate-AverageMInFile
Status : OPTIMAL
Pre-binning statistics
Number of pre-bins 100
Number of refinements 844
Solver statistics
Type mip
Number of variables 1596
Number of constraints 2181
Objective value 1.0983
Best objective bound 1.0983
Timing
Total time 5.78 sec
Pre-processing 0.00 sec ( 0.06%)
Pre-binning 0.02 sec ( 0.28%)
Solver 5.75 sec ( 99.53%)
Post-processing 0.00 sec ( 0.03%)
In this case, the MIP solver reduces the CPU time by 40%. The default strategy to perform refinements is set to strategy="grid". Alternatively, when setting strategy="cart", a decision tree is used to reduce the space search by merging not relevant pre-bins. This procedure accelerates the solution of the optimization problem at the expense of worsening the total IV.
[41]:
optb = OptimalBinning2D(name_x=variable1, name_y=variable2,
solver="cp", strategy="cart",
monotonic_trend_x="descending",
monotonic_trend_y="descending",
max_n_prebins_x=10, max_n_prebins_y=10,
min_bin_size=0.05,
special_codes_x=special_codes_x,
special_codes_y=special_codes_y)
optb.fit(x, y, z)
[41]:
OptimalBinning2D(max_n_prebins_x=10, max_n_prebins_y=10, min_bin_size=0.05,
monotonic_trend_x='descending', monotonic_trend_y='descending',
name_x='ExternalRiskEstimate', name_y='AverageMInFile',
special_codes_x=[-9, -8, -7], special_codes_y=[-9, -8, -7],
strategy='cart')
[42]:
optb.binning_table.build()
[42]:
| Bin x | Bin y | Count | Count (%) | Non-event | Event | Event rate | WoE | IV | JS | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | (-inf, 63.50) | (-inf, 54.50) | 749 | 0.071613 | 87 | 662 | 0.883845 | -1.941530 | 0.201662 | 0.021871 |
| 1 | [63.50, 73.50) | (-inf, 48.50) | 768 | 0.073430 | 181 | 587 | 0.764323 | -1.088700 | 0.077656 | 0.009254 |
| 2 | [73.50, 80.50) | (-inf, 64.50) | 620 | 0.059279 | 324 | 296 | 0.477419 | 0.178212 | 0.001885 | 0.000235 |
| 3 | [80.50, inf) | (-inf, 74.50) | 563 | 0.053829 | 405 | 158 | 0.280639 | 1.029120 | 0.053573 | 0.006416 |
| 4 | [63.50, 73.50) | [48.50, 64.50) | 661 | 0.063199 | 235 | 426 | 0.644478 | -0.507026 | 0.015736 | 0.001946 |
| 5 | (-inf, 59.50) | [54.50, inf) | 746 | 0.071326 | 131 | 615 | 0.824397 | -1.458597 | 0.126107 | 0.014500 |
| 6 | [59.50, 63.50) | [54.50, inf) | 683 | 0.065303 | 176 | 507 | 0.742313 | -0.970199 | 0.055955 | 0.006732 |
| 7 | [63.50, 70.50) | [64.50, inf) | 1314 | 0.125633 | 488 | 826 | 0.628615 | -0.438452 | 0.023549 | 0.002920 |
| 8 | [70.50, 75.50) | [64.50, inf) | 1049 | 0.100296 | 596 | 453 | 0.431840 | 0.362176 | 0.013117 | 0.001631 |
| 9 | [75.50, 80.50) | [64.50, inf) | 960 | 0.091787 | 665 | 295 | 0.307292 | 0.900639 | 0.071115 | 0.008601 |
| 10 | [80.50, 84.50) | [74.50, inf) | 668 | 0.063868 | 528 | 140 | 0.209581 | 1.415282 | 0.113158 | 0.013071 |
| 11 | [84.50, inf) | [74.50, inf) | 1080 | 0.103260 | 917 | 163 | 0.150926 | 1.815185 | 0.278705 | 0.030726 |
| 12 | Special | Special | 598 | 0.057176 | 267 | 331 | 0.553512 | -0.127042 | 0.000919 | 0.000115 |
| 13 | Missing | Missing | 0 | 0.000000 | 0 | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| Totals | 10459 | 1.000000 | 5000 | 5459 | 0.521943 | 1.033139 | 0.118019 |
[43]:
optb.binning_table.plot(metric="event_rate")
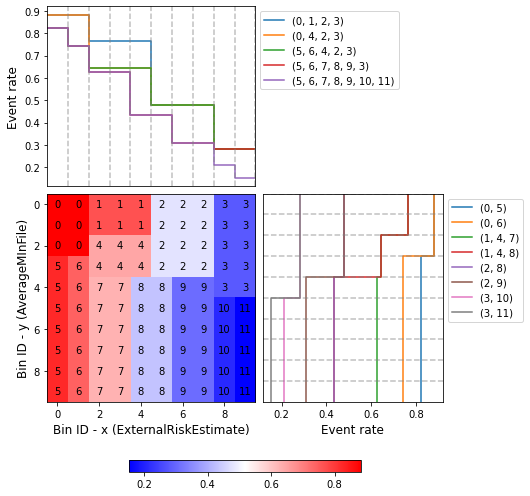
[44]:
optb.information(print_level=1)
optbinning (Version 0.19.0)
Copyright (c) 2019-2024 Guillermo Navas-Palencia, Apache License 2.0
Name : ExternalRiskEstimate-AverageMInFile
Status : OPTIMAL
Pre-binning statistics
Number of pre-bins 100
Number of refinements 2802
Solver statistics
Type cp
Number of booleans 145
Number of branches 1962
Number of conflicts 594
Objective value 1094546
Best objective bound 1094546
Timing
Total time 0.57 sec
Pre-processing 0.00 sec ( 0.40%)
Pre-binning 0.02 sec ( 4.13%)
Solver 0.55 sec ( 95.19%)
model generation 0.38 sec ( 68.68%)
optimizer 0.17 sec ( 31.32%)
Post-processing 0.00 sec ( 0.15%)
We get a 21x speedup at the cost of -0.34% reduction in IV.
20 prebins (400 grid elements)¶
[45]:
optb = OptimalBinning2D(name_x=variable1, name_y=variable2,
solver="cp",
monotonic_trend_x="descending",
monotonic_trend_y="descending",
max_n_prebins_x=20, max_n_prebins_y=20,
min_bin_size=0.05,
special_codes_x=special_codes_x,
special_codes_y=special_codes_y)
optb.fit(x, y, z)
[45]:
OptimalBinning2D(max_n_prebins_x=20, max_n_prebins_y=20, min_bin_size=0.05,
monotonic_trend_x='descending', monotonic_trend_y='descending',
name_x='ExternalRiskEstimate', name_y='AverageMInFile',
special_codes_x=[-9, -8, -7], special_codes_y=[-9, -8, -7])
[46]:
optb.binning_table.build()
[46]:
| Bin x | Bin y | Count | Count (%) | Non-event | Event | Event rate | WoE | IV | JS | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | (-inf, 63.50) | (-inf, 54.50) | 749 | 0.071613 | 87 | 662 | 0.883845 | -1.941530 | 0.201662 | 0.021871 |
| 1 | [63.50, 75.50) | (-inf, 41.50) | 571 | 0.054594 | 141 | 430 | 0.753065 | -1.027198 | 0.051944 | 0.006222 |
| 2 | [75.50, 87.50) | (-inf, 64.50) | 698 | 0.066737 | 413 | 285 | 0.408309 | 0.458786 | 0.013944 | 0.001728 |
| 3 | [87.50, inf) | (-inf, inf) | 616 | 0.058897 | 524 | 92 | 0.149351 | 1.827531 | 0.160726 | 0.017692 |
| 4 | [63.50, 67.50) | [41.50, 74.50) | 550 | 0.052586 | 154 | 396 | 0.720000 | -0.856634 | 0.035757 | 0.004338 |
| 5 | [67.50, 73.50) | [41.50, 64.50) | 548 | 0.052395 | 194 | 354 | 0.645985 | -0.513611 | 0.013378 | 0.001654 |
| 6 | [73.50, 75.50) | [41.50, inf) | 552 | 0.052778 | 314 | 238 | 0.431159 | 0.364950 | 0.007008 | 0.000871 |
| 7 | (-inf, 59.50) | [54.50, inf) | 746 | 0.071326 | 131 | 615 | 0.824397 | -1.458597 | 0.126107 | 0.014500 |
| 8 | [59.50, 63.50) | [54.50, inf) | 683 | 0.065303 | 176 | 507 | 0.742313 | -0.970199 | 0.055955 | 0.006732 |
| 9 | [67.50, 70.50) | [64.50, inf) | 599 | 0.057271 | 256 | 343 | 0.572621 | -0.204725 | 0.002381 | 0.000297 |
| 10 | [70.50, 73.50) | [64.50, inf) | 639 | 0.061096 | 354 | 285 | 0.446009 | 0.304635 | 0.005664 | 0.000705 |
| 11 | [75.50, 80.50) | [64.50, inf) | 960 | 0.091787 | 665 | 295 | 0.307292 | 0.900639 | 0.071115 | 0.008601 |
| 12 | [80.50, 84.50) | [64.50, inf) | 814 | 0.077828 | 636 | 178 | 0.218673 | 1.361243 | 0.128764 | 0.014958 |
| 13 | [84.50, 87.50) | [64.50, inf) | 606 | 0.057941 | 510 | 96 | 0.158416 | 1.757890 | 0.148391 | 0.016478 |
| 14 | [63.50, 67.50) | [74.50, inf) | 530 | 0.050674 | 178 | 352 | 0.664151 | -0.594020 | 0.017156 | 0.002113 |
| 15 | Special | Special | 598 | 0.057176 | 267 | 331 | 0.553512 | -0.127042 | 0.000919 | 0.000115 |
| 16 | Missing | Missing | 0 | 0.000000 | 0 | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| Totals | 10459 | 1.000000 | 5000 | 5459 | 0.521943 | 1.040872 | 0.118874 |
[47]:
optb.information()
optbinning (Version 0.19.0)
Copyright (c) 2019-2024 Guillermo Navas-Palencia, Apache License 2.0
Name : ExternalRiskEstimate-AverageMInFile
Status : OPTIMAL
Pre-binning statistics
Number of pre-bins 168
Number of refinements 2524
Solver statistics
Type cp
Number of booleans 5616
Number of branches 25469
Number of conflicts 13345
Objective value 1102734
Best objective bound 1102734
Timing
Total time 41.69 sec
Pre-processing 0.00 sec ( 0.01%)
Pre-binning 0.02 sec ( 0.04%)
Solver 41.64 sec ( 99.88%)
model generation 16.30 sec ( 39.13%)
optimizer 25.35 sec ( 60.87%)
Post-processing 0.00 sec ( 0.01%)
[48]:
optb = OptimalBinning2D(name_x=variable1, name_y=variable2,
solver="mip",
monotonic_trend_x="descending",
monotonic_trend_y="descending",
max_n_prebins_x=20, max_n_prebins_y=20,
min_bin_size=0.05,
special_codes_x=special_codes_x,
special_codes_y=special_codes_y)
optb.fit(x, y, z)
[48]:
OptimalBinning2D(max_n_prebins_x=20, max_n_prebins_y=20, min_bin_size=0.05,
monotonic_trend_x='descending', monotonic_trend_y='descending',
name_x='ExternalRiskEstimate', name_y='AverageMInFile',
solver='mip', special_codes_x=[-9, -8, -7],
special_codes_y=[-9, -8, -7])
[49]:
optb.information()
optbinning (Version 0.19.0)
Copyright (c) 2019-2024 Guillermo Navas-Palencia, Apache License 2.0
Name : ExternalRiskEstimate-AverageMInFile
Status : OPTIMAL
Pre-binning statistics
Number of pre-bins 168
Number of refinements 2524
Solver statistics
Type mip
Number of variables 4098
Number of constraints 5666
Objective value 1.1027
Best objective bound 1.1027
Timing
Total time 51.33 sec
Pre-processing 0.00 sec ( 0.01%)
Pre-binning 0.02 sec ( 0.04%)
Solver 51.28 sec ( 99.91%)
Post-processing 0.00 sec ( 0.01%)
[50]:
optb = OptimalBinning2D(name_x=variable1, name_y=variable2,
solver="cp", strategy="cart",
monotonic_trend_x="descending",
monotonic_trend_y="descending",
max_n_prebins_x=20, max_n_prebins_y=20,
min_bin_size=0.05,
special_codes_x=special_codes_x,
special_codes_y=special_codes_y)
optb.fit(x, y, z)
[50]:
OptimalBinning2D(max_n_prebins_x=20, max_n_prebins_y=20, min_bin_size=0.05,
monotonic_trend_x='descending', monotonic_trend_y='descending',
name_x='ExternalRiskEstimate', name_y='AverageMInFile',
special_codes_x=[-9, -8, -7], special_codes_y=[-9, -8, -7],
strategy='cart')
[51]:
optb.binning_table.build()
[51]:
| Bin x | Bin y | Count | Count (%) | Non-event | Event | Event rate | WoE | IV | JS | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | (-inf, 63.50) | (-inf, 54.50) | 749 | 0.071613 | 87 | 662 | 0.883845 | -1.941530 | 0.201662 | 0.021871 |
| 1 | [63.50, 67.50) | (-inf, 69.50) | 713 | 0.068171 | 182 | 531 | 0.744741 | -0.982928 | 0.059831 | 0.007192 |
| 2 | [67.50, 73.50) | (-inf, 64.50) | 811 | 0.077541 | 263 | 548 | 0.675709 | -0.646294 | 0.030883 | 0.003795 |
| 3 | [73.50, 80.50) | (-inf, 64.50) | 620 | 0.059279 | 324 | 296 | 0.477419 | 0.178212 | 0.001885 | 0.000235 |
| 4 | [80.50, 84.50) | (-inf, 97.50) | 726 | 0.069414 | 533 | 193 | 0.265840 | 1.103659 | 0.078631 | 0.009359 |
| 5 | [84.50, inf) | (-inf, 97.50) | 615 | 0.058801 | 511 | 104 | 0.169106 | 1.679806 | 0.139674 | 0.015658 |
| 6 | (-inf, 59.50) | [54.50, inf) | 746 | 0.071326 | 131 | 615 | 0.824397 | -1.458597 | 0.126107 | 0.014500 |
| 7 | [59.50, 63.50) | [54.50, inf) | 683 | 0.065303 | 176 | 507 | 0.742313 | -0.970199 | 0.055955 | 0.006732 |
| 8 | [67.50, 70.50) | [64.50, inf) | 599 | 0.057271 | 256 | 343 | 0.572621 | -0.204725 | 0.002381 | 0.000297 |
| 9 | [70.50, 75.50) | [64.50, inf) | 1049 | 0.100296 | 596 | 453 | 0.431840 | 0.362176 | 0.013117 | 0.001631 |
| 10 | [75.50, 80.50) | [64.50, inf) | 960 | 0.091787 | 665 | 295 | 0.307292 | 0.900639 | 0.071115 | 0.008601 |
| 11 | [63.50, 67.50) | [69.50, inf) | 620 | 0.059279 | 203 | 417 | 0.672581 | -0.632053 | 0.022620 | 0.002781 |
| 12 | [80.50, inf) | [97.50, inf) | 970 | 0.092743 | 806 | 164 | 0.169072 | 1.680045 | 0.220351 | 0.024702 |
| 13 | Special | Special | 598 | 0.057176 | 267 | 331 | 0.553512 | -0.127042 | 0.000919 | 0.000115 |
| 14 | Missing | Missing | 0 | 0.000000 | 0 | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| Totals | 10459 | 1.000000 | 5000 | 5459 | 0.521943 | 1.025133 | 0.117469 |
[52]:
optb.binning_table.plot(metric="event_rate")
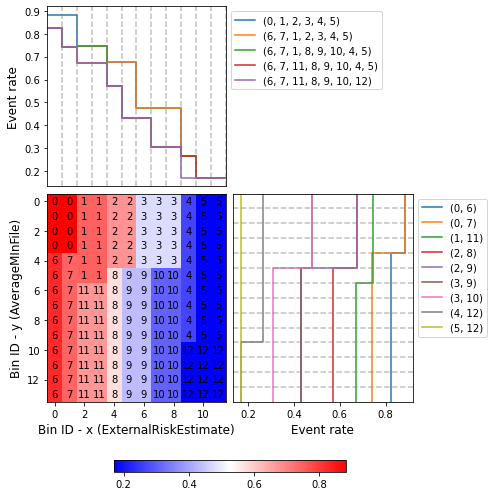
[53]:
optb.information()
optbinning (Version 0.19.0)
Copyright (c) 2019-2024 Guillermo Navas-Palencia, Apache License 2.0
Name : ExternalRiskEstimate-AverageMInFile
Status : OPTIMAL
Pre-binning statistics
Number of pre-bins 168
Number of refinements 8046
Solver statistics
Type cp
Number of booleans 51
Number of branches 127
Number of conflicts 5
Objective value 1086067
Best objective bound 1086067
Timing
Total time 0.74 sec
Pre-processing 0.00 sec ( 0.53%)
Pre-binning 0.02 sec ( 3.00%)
Solver 0.71 sec ( 96.12%)
model generation 0.69 sec ( 97.08%)
optimizer 0.02 sec ( 2.92%)
Post-processing 0.00 sec ( 0.19%)
We get a 58x speedup at the cost of -1.51% reduction in IV. The following table summarizes performance improvements:
prebins |
CP + grid |
MIP + grid |
CP + cart |
Speedup CP |
Speed MIP |
|---|---|---|---|---|---|
10 (100) |
11.40 s |
5.97 s |
0.69 s |
17x |
9x |
20 (400) |
52.76 s |
52.93 s |
0.74 s |
71x |
72x |
Categorical variables¶
The combination of categorical-categorical and numerical-categorical are supported since version 0.15.0.
[54]:
df = pd.read_csv("data/kaggle/HomeCreditDefaultRisk/application_train.csv",
engine='c')
Case categorical-categorical
[55]:
variable1 = "ORGANIZATION_TYPE"
variable2 = "NAME_INCOME_TYPE"
x = df[variable1].values
y = df[variable2].values
z = df["TARGET"].values
[56]:
optb = OptimalBinning2D(name_x=variable1, name_y=variable2,
dtype_x="categorical", dtype_y="categorical",
max_n_bins=10)
optb.fit(x, y, z)
[56]:
OptimalBinning2D(dtype_x='categorical', dtype_y='categorical', max_n_bins=10,
name_x='ORGANIZATION_TYPE', name_y='NAME_INCOME_TYPE')
[57]:
optb.binning_table.build(show_bin_xy=True)
[57]:
| Bin | Count | Count (%) | Non-event | Event | Event rate | WoE | IV | JS | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | ['Trade: type 4' 'Industry: type 12' 'Transpor... | 55390 | 0.180124 | 52408 | 2982 | 0.053836 | 0.433980 | 0.028327 | 0.003513 |
| 1 | ['Trade: type 4' 'Industry: type 12' 'Transpor... | 11442 | 0.037208 | 10891 | 551 | 0.048156 | 0.551472 | 0.009006 | 0.001112 |
| 2 | ['Hotel' 'Industry: type 10' 'Medicine' 'Servi... | 23267 | 0.075662 | 21865 | 1402 | 0.060257 | 0.314502 | 0.006564 | 0.000817 |
| 3 | ['Housing' 'Industry: type 7' 'Business Entity... | 38863 | 0.126379 | 35966 | 2897 | 0.074544 | 0.086413 | 0.000910 | 0.000114 |
| 4 | ['Security' 'Industry: type 4' 'Self-employed'... | 19748 | 0.064219 | 17989 | 1759 | 0.089072 | -0.107471 | 0.000776 | 0.000097 |
| 5 | ['Trade: type 4' 'Industry: type 12' 'Transpor... | 10624 | 0.034548 | 9981 | 643 | 0.060523 | 0.309808 | 0.002914 | 0.000363 |
| 6 | ['Hotel' 'Industry: type 10' 'Medicine' 'Servi... | 35568 | 0.115664 | 32792 | 2776 | 0.078048 | 0.036688 | 0.000153 | 0.000019 |
| 7 | ['Housing' 'Industry: type 7' 'Business Entity... | 69102 | 0.224714 | 62197 | 6905 | 0.099925 | -0.234425 | 0.013626 | 0.001699 |
| 8 | ['Security' 'Industry: type 4' 'Self-employed'... | 31207 | 0.101483 | 27795 | 3412 | 0.109334 | -0.334928 | 0.013102 | 0.001630 |
| 9 | ['Agriculture' 'Realtor' 'Industry: type 3' 'I... | 12300 | 0.039999 | 10802 | 1498 | 0.121789 | -0.456885 | 0.010111 | 0.001253 |
| 10 | Special | 0 | 0.000000 | 0 | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 11 | Missing | 0 | 0.000000 | 0 | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| Totals | 307511 | 1.000000 | 282686 | 24825 | 0.080729 | 0.085490 | 0.010617 |
[58]:
optb.splits
[58]:
([array(['Trade: type 4', 'Industry: type 12', 'Transport: type 1',
'Trade: type 6', 'Security Ministries', 'University', 'Police',
'Military', 'Bank', 'XNA', 'Culture', 'Insurance', 'Religion',
'School', 'Trade: type 5', 'Hotel', 'Industry: type 10',
'Medicine', 'Services', 'Electricity', 'Industry: type 9',
'Industry: type 5', 'Government', 'Trade: type 2', 'Kindergarten',
'Emergency', 'Industry: type 6', 'Industry: type 2', 'Telecom',
'Other', 'Transport: type 2', 'Legal Services', 'Housing',
'Industry: type 7', 'Business Entity Type 1', 'Advertising',
'Postal', 'Business Entity Type 2', 'Industry: type 11',
'Trade: type 1', 'Mobile', 'Transport: type 4',
'Business Entity Type 3', 'Trade: type 7', 'Security',
'Industry: type 4', 'Self-employed', 'Trade: type 3',
'Agriculture', 'Realtor', 'Industry: type 3', 'Industry: type 1',
'Cleaning', 'Construction', 'Restaurant', 'Industry: type 8',
'Industry: type 13', 'Transport: type 3'], dtype=object),
array(['Trade: type 4', 'Industry: type 12', 'Transport: type 1',
'Trade: type 6', 'Security Ministries', 'University', 'Police',
'Military', 'Bank', 'XNA', 'Culture', 'Insurance', 'Religion',
'School', 'Trade: type 5'], dtype=object),
array(['Hotel', 'Industry: type 10', 'Medicine', 'Services',
'Electricity', 'Industry: type 9', 'Industry: type 5',
'Government', 'Trade: type 2', 'Kindergarten', 'Emergency',
'Industry: type 6', 'Industry: type 2', 'Telecom', 'Other',
'Transport: type 2', 'Legal Services'], dtype=object),
array(['Housing', 'Industry: type 7', 'Business Entity Type 1',
'Advertising', 'Postal', 'Business Entity Type 2',
'Industry: type 11', 'Trade: type 1', 'Mobile',
'Transport: type 4', 'Business Entity Type 3', 'Trade: type 7'],
dtype=object),
array(['Security', 'Industry: type 4', 'Self-employed', 'Trade: type 3',
'Agriculture', 'Realtor', 'Industry: type 3', 'Industry: type 1',
'Cleaning', 'Construction', 'Restaurant', 'Industry: type 8',
'Industry: type 13', 'Transport: type 3'], dtype=object),
array(['Trade: type 4', 'Industry: type 12', 'Transport: type 1',
'Trade: type 6', 'Security Ministries', 'University', 'Police',
'Military', 'Bank', 'XNA', 'Culture', 'Insurance', 'Religion',
'School', 'Trade: type 5'], dtype=object),
array(['Hotel', 'Industry: type 10', 'Medicine', 'Services',
'Electricity', 'Industry: type 9', 'Industry: type 5',
'Government', 'Trade: type 2', 'Kindergarten', 'Emergency',
'Industry: type 6', 'Industry: type 2', 'Telecom', 'Other',
'Transport: type 2', 'Legal Services'], dtype=object),
array(['Housing', 'Industry: type 7', 'Business Entity Type 1',
'Advertising', 'Postal', 'Business Entity Type 2',
'Industry: type 11', 'Trade: type 1', 'Mobile',
'Transport: type 4', 'Business Entity Type 3', 'Trade: type 7'],
dtype=object),
array(['Security', 'Industry: type 4', 'Self-employed', 'Trade: type 3'],
dtype=object),
array(['Agriculture', 'Realtor', 'Industry: type 3', 'Industry: type 1',
'Cleaning', 'Construction', 'Restaurant', 'Industry: type 8',
'Industry: type 13', 'Transport: type 3'], dtype=object)],
[array(['Businessman', 'Student', 'Pensioner'], dtype=object),
array(['State servant', 'Commercial associate'], dtype=object),
array(['State servant', 'Commercial associate'], dtype=object),
array(['State servant', 'Commercial associate'], dtype=object),
array(['State servant', 'Commercial associate'], dtype=object),
array(['Working', 'Unemployed', 'Maternity leave'], dtype=object),
array(['Working', 'Unemployed', 'Maternity leave'], dtype=object),
array(['Working', 'Unemployed', 'Maternity leave'], dtype=object),
array(['Working', 'Unemployed', 'Maternity leave'], dtype=object),
array(['Working', 'Unemployed', 'Maternity leave'], dtype=object)])
[59]:
optb.binning_table.plot(metric="event_rate")
[60]:
z_transform_woe = optb.transform(x, y, metric="woe")
pd.Series(z_transform_woe).value_counts()
[60]:
-0.234425 69102
0.433980 55390
0.086413 38863
0.036688 35568
-0.334928 31207
0.314502 23267
-0.107471 19748
-0.456885 12300
0.551472 11442
0.309808 10624
dtype: int64
[61]:
z_transform_indices = optb.transform(x, y, metric="indices")
pd.Series(z_transform_indices).value_counts()
[61]:
7 69102
0 55390
3 38863
6 35568
8 31207
2 23267
4 19748
9 12300
1 11442
5 10624
dtype: int64
Case numerical-categorical
[62]:
variable1 = "AMT_INCOME_TOTAL"
variable2 = "NAME_INCOME_TYPE"
x = df[variable1].values
y = df[variable2].values
[63]:
optb = OptimalBinning2D(name_x=variable1, name_y=variable2,
dtype_x="numerical", dtype_y="categorical",
monotonic_trend_x="descending",
monotonic_trend_y="ascending")
optb.fit(x, y, z)
[63]:
OptimalBinning2D(dtype_y='categorical', monotonic_trend_x='descending',
monotonic_trend_y='ascending', name_x='AMT_INCOME_TOTAL',
name_y='NAME_INCOME_TYPE')
[64]:
optb.binning_table.build(show_bin_xy=True)
[64]:
| Bin | Count | Count (%) | Non-event | Event | Event rate | WoE | IV | JS | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | (-inf, 184511.25) $\cup$ ['Businessman' 'Stude... | 45526 | 0.148047 | 43045 | 2481 | 0.054496 | 0.421099 | 0.022037 | 0.002734 |
| 1 | [184511.25, 232717.50) $\cup$ ['Businessman' '... | 5400 | 0.017560 | 5121 | 279 | 0.051667 | 0.477408 | 0.003283 | 0.000407 |
| 2 | [232717.50, 310950.00) $\cup$ ['Businessman' '... | 4955 | 0.016113 | 4723 | 232 | 0.046821 | 0.580977 | 0.004277 | 0.000527 |
| 3 | [310950.00, inf) $\cup$ ['Businessman' 'Studen... | 3723 | 0.012107 | 3570 | 153 | 0.041096 | 0.717397 | 0.004638 | 0.000568 |
| 4 | (-inf, 76477.50) $\cup$ ['State servant'] | 1299 | 0.004224 | 1206 | 93 | 0.071594 | 0.129979 | 0.000068 | 0.000008 |
| 5 | [76477.50, 184511.25) $\cup$ ['State servant'] | 12623 | 0.041049 | 11820 | 803 | 0.063614 | 0.256708 | 0.002430 | 0.000303 |
| 6 | [184511.25, 232717.50) $\cup$ ['State servant'] | 3567 | 0.011600 | 3377 | 190 | 0.053266 | 0.445233 | 0.001911 | 0.000237 |
| 7 | (-inf, 76477.50) $\cup$ ['Commercial associate'] | 1917 | 0.006234 | 1734 | 183 | 0.095462 | -0.183786 | 0.000227 | 0.000028 |
| 8 | [76477.50, 184511.25) $\cup$ ['Commercial asso... | 39005 | 0.126841 | 35809 | 3196 | 0.081938 | -0.016186 | 0.000033 | 0.000004 |
| 9 | [184511.25, 232717.50) $\cup$ ['Commercial ass... | 12996 | 0.042262 | 12079 | 917 | 0.070560 | 0.145631 | 0.000843 | 0.000105 |
| 10 | [232717.50, 310950.00) $\cup$ ['Commercial ass... | 8090 | 0.026308 | 7558 | 532 | 0.065760 | 0.221233 | 0.001174 | 0.000146 |
| 11 | [310950.00, inf) $\cup$ ['Commercial associate'] | 9609 | 0.031248 | 9077 | 532 | 0.055365 | 0.404370 | 0.004319 | 0.000536 |
| 12 | (-inf, 76477.50) $\cup$ ['Working' 'Unemployed... | 10879 | 0.035378 | 9786 | 1093 | 0.100469 | -0.240459 | 0.002263 | 0.000282 |
| 13 | [76477.50, 184511.25) $\cup$ ['Working' 'Unemp... | 104920 | 0.341191 | 94465 | 10455 | 0.099647 | -0.231336 | 0.020121 | 0.002510 |
| 14 | [184511.25, 232717.50) $\cup$ ['Working' 'Unem... | 22580 | 0.073428 | 20492 | 2088 | 0.092471 | -0.148658 | 0.001727 | 0.000216 |
| 15 | [232717.50, 310950.00) $\cup$ ['Working' 'Unem... | 11666 | 0.037937 | 10688 | 978 | 0.083833 | -0.041118 | 0.000065 | 0.000008 |
| 16 | [310950.00, inf) $\cup$ ['Working' 'Unemployed... | 8756 | 0.028474 | 8136 | 620 | 0.070809 | 0.141849 | 0.000540 | 0.000067 |
| 17 | Special | 0 | 0.000000 | 0 | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 18 | Missing | 0 | 0.000000 | 0 | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| Totals | 307511 | 1.000000 | 282686 | 24825 | 0.080729 | 0.069958 | 0.008688 |
[65]:
optb.binning_table.plot(metric="event_rate")
[66]:
z_transform_woe = optb.transform(x, y, metric="woe")
pd.Series(z_transform_woe).value_counts()
[66]:
-0.231336 104920
0.421099 45526
-0.016186 39005
-0.148658 22580
0.145631 12996
0.256708 12623
-0.041118 11666
-0.240459 10879
0.404370 9609
0.141849 8756
0.221233 8090
0.477408 5400
0.580977 4955
0.717397 3723
0.445233 3567
-0.183786 1917
0.129979 1299
dtype: int64
[67]:
z_transform_indices = optb.transform(x, y, metric="indices")
pd.Series(z_transform_indices).value_counts()
[67]:
13 104920
0 45526
8 39005
14 22580
9 12996
5 12623
15 11666
12 10879
11 9609
16 8756
10 8090
1 5400
2 4955
3 3723
6 3567
7 1917
4 1299
dtype: int64