Tutorial: FICO Explainable Machine Learning Challenge - Updating Binning¶
In this tutorial, we extend the previous tutorial using the FICO dataset by replacing the usual binning with a piecewise continuous binning. The piecewise continuous binning uses a Gradient Boosting Tree (GBT) as an estimator.
[1]:
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
[2]:
from lightgbm import LGBMClassifier
from optbinning import BinningProcess
from optbinning import OptimalPWBinning
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.metrics import classification_report
from sklearn.metrics import auc, roc_auc_score, roc_curve
from sklearn.model_selection import train_test_split
Download the dataset from the link above and load it: https://community.fico.com/s/explainable-machine-learning-challenge.
[3]:
df = pd.read_csv("data/FICO_challenge/heloc_dataset_v1.csv", sep=",")
variable_names = list(df.columns[1:])
X = df[variable_names]
Transform the categorical dichotomic target variable into numerical.
[4]:
y = df.RiskPerformance.values
mask = y == "Bad"
y[mask] = 1
y[~mask] = 0
y = y.astype(int)
Modeling¶
The data dictionary of this challenge includes three special values/codes:
-9 No Bureau Record or No Investigation
-8 No Usable/Valid Trades or Inquiries
-7 Condition not Met (e.g. No Inquiries, No Delinquencies)
[5]:
special_codes = [-9, -8, -7]
This challenge imposes monotonicity constraints with respect to the probability of a bad target for many of the variables. We apply these rules by passing the following dictionary of parameters for these variables involved.
[6]:
binning_fit_params = {
"ExternalRiskEstimate": {"monotonic_trend": "descending"},
"MSinceOldestTradeOpen": {"monotonic_trend": "descending"},
"MSinceMostRecentTradeOpen": {"monotonic_trend": "descending"},
"AverageMInFile": {"monotonic_trend": "descending"},
"NumSatisfactoryTrades": {"monotonic_trend": "descending"},
"NumTrades60Ever2DerogPubRec": {"monotonic_trend": "ascending"},
"NumTrades90Ever2DerogPubRec": {"monotonic_trend": "ascending"},
"PercentTradesNeverDelq": {"monotonic_trend": "descending"},
"MSinceMostRecentDelq": {"monotonic_trend": "descending"},
"NumTradesOpeninLast12M": {"monotonic_trend": "ascending"},
"MSinceMostRecentInqexcl7days": {"monotonic_trend": "descending"},
"NumInqLast6M": {"monotonic_trend": "ascending"},
"NumInqLast6Mexcl7days": {"monotonic_trend": "ascending"},
"NetFractionRevolvingBurden": {"monotonic_trend": "ascending"},
"NetFractionInstallBurden": {"monotonic_trend": "ascending"},
"NumBank2NatlTradesWHighUtilization": {"monotonic_trend": "ascending"}
}
Instantiate a BinningProcess object class with variable names, special codes and dictionary of binning parameters. Choose a logistic regression as a classifier.
[7]:
binning_process = BinningProcess(variable_names, special_codes=special_codes,
binning_fit_params=binning_fit_params)
[8]:
clf = LogisticRegression(solver="lbfgs")
Split dataset into train and test. Fit pipelines with training data, then generate classification reports to show the main classification metrics.
[9]:
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
[10]:
binning_process.fit(X_train, y_train)
[10]:
BinningProcess(binning_fit_params={'AverageMInFile': {'monotonic_trend': 'descending'},
'ExternalRiskEstimate': {'monotonic_trend': 'descending'},
'MSinceMostRecentDelq': {'monotonic_trend': 'descending'},
'MSinceMostRecentInqexcl7days': {'monotonic_trend': 'descending'},
'MSinceMostRecentTradeOpen': {'monotonic_trend': 'descending'},
'MSinceOldestTradeOpen': {'mo...
'MaxDelq2PublicRecLast12M', 'MaxDelqEver',
'NumTotalTrades', 'NumTradesOpeninLast12M',
'PercentInstallTrades',
'MSinceMostRecentInqexcl7days', 'NumInqLast6M',
'NumInqLast6Mexcl7days',
'NetFractionRevolvingBurden',
'NetFractionInstallBurden',
'NumRevolvingTradesWBalance',
'NumInstallTradesWBalance',
'NumBank2NatlTradesWHighUtilization',
'PercentTradesWBalance'])
Now, we replace the usual binning of a few numerical variables with a piecewise continuous binning. Since version 0.9.2, the binning process includes the method update_binned_variable which allows updating an optimal binning without the need of re-processing the rest of the variables.
[11]:
update_variables = ["ExternalRiskEstimate", "MSinceOldestTradeOpen", "PercentTradesWBalance"]
for variable in update_variables:
optb = OptimalPWBinning(estimator=LGBMClassifier(),
name=variable, objective="l1")
optb.fit(X_train[variable], y_train, lb=0.001, ub=0.999)
binning_process.update_binned_variable(name=variable, optb=optb)
Performance¶
[12]:
clf.fit(binning_process.transform(X_train), y_train)
/home/gui/projects/github/top/optbinning/optbinning/binning/transformations.py:38: RuntimeWarning: invalid value encountered in log
return np.log((1. / event_rate - 1) * n_event / n_nonevent)
[12]:
LogisticRegression()
[13]:
y_pred = clf.predict(binning_process.transform(X_test))
print(classification_report(y_test, y_pred))
precision recall f1-score support
0 0.71 0.67 0.69 1004
1 0.71 0.74 0.73 1088
accuracy 0.71 2092
macro avg 0.71 0.71 0.71 2092
weighted avg 0.71 0.71 0.71 2092
/home/gui/projects/github/top/optbinning/optbinning/binning/transformations.py:38: RuntimeWarning: invalid value encountered in log
return np.log((1. / event_rate - 1) * n_event / n_nonevent)
If we compare with the results from the previous tutorial, we observe a slight improvement in all three metrics.
[14]:
probs = clf.predict_proba(binning_process.transform(X_test))
preds = probs[:,1]
fpr1, tpr1, threshold = roc_curve(y_test, preds)
roc_auc1 = auc(fpr1, tpr1)
/home/gui/projects/github/top/optbinning/optbinning/binning/transformations.py:38: RuntimeWarning: invalid value encountered in log
return np.log((1. / event_rate - 1) * n_event / n_nonevent)
[15]:
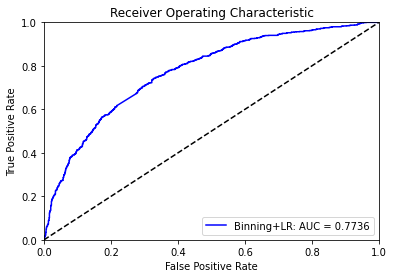
plt.title('Receiver Operating Characteristic')
plt.plot(fpr1, tpr1, 'b', label='Binning+LR: AUC = {0:.4f}'.format(roc_auc1))
plt.legend(loc='lower right')
plt.plot([0, 1], [0, 1],'k--')
plt.xlim([0, 1])
plt.ylim([0, 1])
plt.ylabel('True Positive Rate')
plt.xlabel('False Positive Rate')
plt.show()
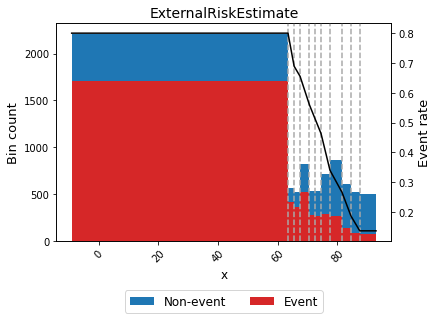
Finally, let’s check the piecewise continuous binning for one of the variables with more importance.
[16]:
optb = binning_process.get_binned_variable("ExternalRiskEstimate")
optb.binning_table.build()
[16]:
| Bin | Count | Count (%) | Non-event | Event | c0 | c1 | |
|---|---|---|---|---|---|---|---|
| 0 | (-inf, 63.50) | 2213 | 0.264491 | 510 | 1703 | 0.799992 | -0.000000 |
| 1 | [63.50, 65.50) | 563 | 0.067288 | 153 | 410 | 4.297026 | -0.055071 |
| 2 | [65.50, 67.50) | 516 | 0.061671 | 157 | 359 | 1.785820 | -0.016732 |
| 3 | [67.50, 70.50) | 824 | 0.098482 | 307 | 517 | 2.741859 | -0.030896 |
| 4 | [70.50, 72.50) | 530 | 0.063344 | 258 | 272 | 2.295900 | -0.024570 |
| 5 | [72.50, 74.50) | 530 | 0.063344 | 265 | 265 | 2.285756 | -0.024430 |
| 6 | [74.50, 77.50) | 709 | 0.084738 | 423 | 286 | 3.568860 | -0.041653 |
| 7 | [77.50, 81.50) | 864 | 0.103263 | 600 | 264 | 1.746868 | -0.018144 |
| 8 | [81.50, 84.50) | 602 | 0.071949 | 461 | 141 | 2.452263 | -0.026799 |
| 9 | [84.50, 87.50) | 518 | 0.061910 | 437 | 81 | 1.635270 | -0.017130 |
| 10 | [87.50, inf) | 498 | 0.059520 | 425 | 73 | 0.136375 | 0.000000 |
| 11 | Special | 0 | 0.000000 | 0 | 0 | 0.000000 | 0.000000 |
| 12 | Missing | 0 | 0.000000 | 0 | 0 | 0.000000 | 0.000000 |
| Totals | 8367 | 1.000000 | 3996 | 4371 | - | - |
[17]:
optb.binning_table.analysis()
---------------------------------------------
OptimalBinning: Binary Binning Table Analysis
---------------------------------------------
General metrics
Gini index 0.49858632
IV (Jeffrey) 1.02947580
JS (Jensen-Shannon) 0.11880544
Hellinger 0.12345593
Triangular 0.44355312
KS 0.40217895
Avg precision 0.69910615
Brier score 0.19906996
HHI 0.12640619
HHI (normalized) 0.05360671
Cramer's V 0.45085066
Quality score 0.01103754
Significance tests
Bin A Bin B t-statistic p-value P[A > B] P[B > A]
0 1 4.273551 0.038710 0.979402 0.020598
1 2 1.388516 0.238656 0.880875 0.119125
2 3 6.506519 0.010748 0.995084 0.004916
3 4 17.292596 0.000032 0.999996 0.000004
4 5 0.184590 0.667458 0.666430 0.333570
5 6 11.450667 0.000715 0.999713 0.000287
6 7 16.377781 0.000052 0.999986 0.000014
7 8 8.982480 0.002726 0.999028 0.000972
8 9 10.554598 0.001159 0.999629 0.000371
9 10 0.186908 0.665503 0.667979 0.332021
[18]:
optb.binning_table.plot(metric="event_rate")
[19]:
binning_process.summary()
[19]:
| name | dtype | status | selected | n_bins | iv | js | gini | quality_score | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | ExternalRiskEstimate | numerical | OPTIMAL | True | 11 | 1.029476 | 0.118805 | 0.498586 | 0.011038 |
| 1 | MSinceOldestTradeOpen | numerical | OPTIMAL | True | 10 | 0.228822 | 0.028029 | 0.241497 | 0.013902 |
| 2 | MSinceMostRecentTradeOpen | numerical | OPTIMAL | True | 6 | 0.019086 | 0.002377 | 0.065597 | 0.000556 |
| 3 | AverageMInFile | numerical | OPTIMAL | True | 10 | 0.319379 | 0.038458 | 0.304157 | 0.128082 |
| 4 | NumSatisfactoryTrades | numerical | OPTIMAL | True | 10 | 0.126726 | 0.015424 | 0.180888 | 0.001210 |
| 5 | NumTrades60Ever2DerogPubRec | numerical | OPTIMAL | True | 4 | 0.178710 | 0.021915 | 0.200184 | 0.201631 |
| 6 | NumTrades90Ever2DerogPubRec | numerical | OPTIMAL | True | 3 | 0.133485 | 0.016301 | 0.155193 | 0.286527 |
| 7 | PercentTradesNeverDelq | numerical | OPTIMAL | True | 8 | 0.377803 | 0.045428 | 0.316946 | 0.101421 |
| 8 | MSinceMostRecentDelq | numerical | OPTIMAL | True | 7 | 0.289526 | 0.035246 | 0.272229 | 0.239494 |
| 9 | MaxDelq2PublicRecLast12M | numerical | OPTIMAL | True | 3 | 0.330280 | 0.040250 | 0.301670 | 0.833712 |
| 10 | MaxDelqEver | numerical | OPTIMAL | True | 4 | 0.236098 | 0.029129 | 0.257314 | 0.667940 |
| 11 | NumTotalTrades | numerical | OPTIMAL | True | 8 | 0.064716 | 0.008027 | 0.138545 | 0.011755 |
| 12 | NumTradesOpeninLast12M | numerical | OPTIMAL | True | 6 | 0.023530 | 0.002936 | 0.083770 | 0.007932 |
| 13 | PercentInstallTrades | numerical | OPTIMAL | True | 8 | 0.098610 | 0.012107 | 0.159569 | 0.077405 |
| 14 | MSinceMostRecentInqexcl7days | numerical | OPTIMAL | True | 4 | 0.166538 | 0.020460 | 0.211639 | 0.531041 |
| 15 | NumInqLast6M | numerical | OPTIMAL | True | 4 | 0.089956 | 0.011127 | 0.159369 | 0.323780 |
| 16 | NumInqLast6Mexcl7days | numerical | OPTIMAL | True | 5 | 0.083992 | 0.010394 | 0.153641 | 0.036291 |
| 17 | NetFractionRevolvingBurden | numerical | OPTIMAL | True | 9 | 0.574686 | 0.068232 | 0.410605 | 0.343593 |
| 18 | NetFractionInstallBurden | numerical | OPTIMAL | True | 5 | 0.037879 | 0.004724 | 0.105916 | 0.053723 |
| 19 | NumRevolvingTradesWBalance | numerical | OPTIMAL | True | 7 | 0.093376 | 0.011578 | 0.162108 | 0.011291 |
| 20 | NumInstallTradesWBalance | numerical | OPTIMAL | True | 5 | 0.014121 | 0.001762 | 0.059437 | 0.010423 |
| 21 | NumBank2NatlTradesWHighUtilization | numerical | OPTIMAL | True | 5 | 0.334853 | 0.041017 | 0.308402 | 0.222126 |
| 22 | PercentTradesWBalance | numerical | OPTIMAL | True | 13 | 0.379001 | 0.045810 | 0.333979 | 0.018258 |