Tutorial¶
[1]:
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.datasets import fetch_california_housing
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import KBinsDiscretizer
[2]:
from ropwr import RobustPWRegression
from optbinning.binning.outlier import RangeDetector
Basic¶
To get us started, let’s load a well-known dataset from the UCI repository and transform the data into a pandas.DataFrame.
[3]:
class Data:
def __init__(self, data, target, feature_names):
self.data = data
self.target = target
self.feature_names = feature_names
def load_boston():
data_url = "http://lib.stat.cmu.edu/datasets/boston"
raw_df = pd.read_csv(data_url, sep=r"\s+", skiprows=22, header=None)
raw_data = np.hstack([raw_df.values[::2, :], raw_df.values[1::2, :2]])
target = raw_df.values[1::2, 2]
feature_names = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS',
'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT']
return Data(raw_data, target, feature_names)
[4]:
data = load_boston()
df = pd.DataFrame(data.data, columns=data.feature_names)
To ease the representation of the solution and performance metrics, we use the following auxiliary function.
[5]:
def report(x, y, pw, splits, alpha=0.5):
idx = np.argsort(x)
xs = x[idx]
ys = y[idx]
pred = pw.predict(xs)
mse = mean_squared_error(y_true=ys, y_pred=pred)
mae = mean_absolute_error(y_true=ys, y_pred=pred)
plt.plot(xs, ys, 'o', alpha=alpha)
plt.plot(xs, pred, '-', linewidth=2, label=f"MSE={mse:.3f}. MAE={mae:.3f}")
for s in splits:
plt.axvline(s, color="grey", linestyle="--")
plt.legend()
plt.show()
Until version 0.3.0 the user was required to provide a list of split points. Since version 0.4.0 two unsupervised binning techniques, equal-size (“uniform”) and equal-frequency interval (“quantile”) from scikit-learn KBinsDiscretizer are available. To make this tutorial compatible with previous versions, we compute the split points externally.
[6]:
variable = "AGE"
x = df[variable].values
y = data.target
[7]:
est = KBinsDiscretizer(n_bins=10, strategy="quantile")
est.fit(x.reshape(-1, 1), y)
splits = est.bin_edges_[0][1:-1]
There are 9 split points, therefore 10 bins.
[8]:
splits
[8]:
array([26.95, 37.8 , 52.4 , 65.4 , 77.5 , 85.9 , 91.8 , 95.6 , 98.8 ])
Import and instantiate an RobustPWRegression object class. Then we call fit with arrays x, y and splits.
[9]:
pw = RobustPWRegression()
[10]:
pw.fit(x, y, splits)
[10]:
RobustPWRegression()
The attribute coef_returns the coefficients of the piecewise regression for each bin.
[11]:
pw.coef_
[11]:
array([[ 2.63677424e+01, 8.02505909e-02],
[ 3.54433847e+01, -2.56507939e-01],
[ 2.81643952e+01, -6.39420794e-02],
[ 2.28603838e+01, 3.72795133e-02],
[ 4.20632314e+01, -2.56342009e-01],
[ 3.10243037e+01, -1.13904232e-01],
[ 2.00180639e+01, 1.42242861e-02],
[ 1.14218262e+02, -1.01192166e+00],
[ 1.97364661e+01, -2.36183578e-02],
[ 6.16982408e+01, -4.48332677e-01]])
[12]:
report(x, y, pw, splits)
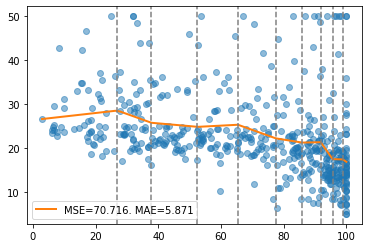
By default, a continuous piecewise regression is fitted, however, this constraint can be deactivated using continuous=False.
[13]:
pw = RobustPWRegression(continuous=False)
pw.fit(x, y, splits=splits)
[13]:
RobustPWRegression(continuous=False)
[14]:
report(x, y, pw, splits)
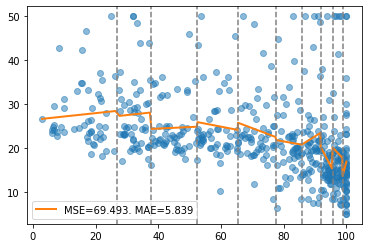
Monotonicity¶
In many applications, it is required to impose certain monotonicity constraints on some features. Six monotonic trends are considered: ascending, descending, convex, concave, peak and valley.
Version 1.0.0 introduced the option to fit a smooth degree \(d\)-polynomial with \(d-1\) continuity in derivatives (splines). By default continuous_deriv is set to True.
In the following, we minimize the \(l_1-\)norm with a quadratic function impose descending monotonicity.
[15]:
pw = RobustPWRegression(objective="l1", degree=2, continuous_deriv=False,
monotonic_trend="descending")
pw.fit(x, y, splits)
[15]:
RobustPWRegression(continuous_deriv=False, degree=2,
monotonic_trend='descending', objective='l1')
[16]:
report(x, y, pw, splits)
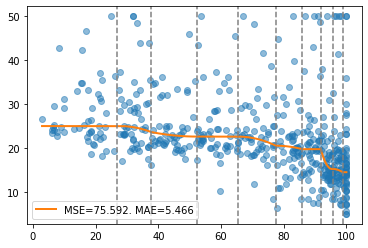
Similar, using the Huber function as an objective.
[17]:
pw = RobustPWRegression(objective="huber", degree=2, continuous_deriv=False,
monotonic_trend="descending")
pw.fit(x, y, splits)
[17]:
RobustPWRegression(continuous_deriv=False, degree=2,
monotonic_trend='descending', objective='huber')
[18]:
report(x, y, pw, splits)
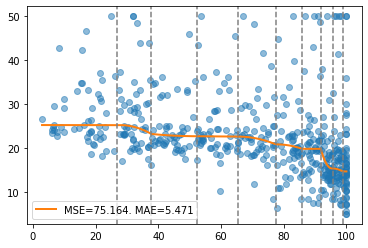
Now, we select a different variable for testing other basic options. This variable shows a less steady relationship with the target.
[19]:
variable = "NOX"
x = df[variable].values
y = data.target
[20]:
est = KBinsDiscretizer(n_bins=10, strategy="quantile")
est.fit(x.reshape(-1, 1), y)
splits = est.bin_edges_[0][1:-1]
[21]:
pw = RobustPWRegression(objective="l2", degree=1, monotonic_trend=None)
pw.fit(x, y, splits)
[21]:
RobustPWRegression()
[22]:
report(x, y, pw, splits)
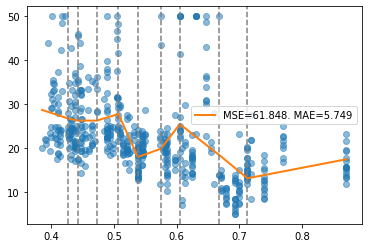
The relationship with the target exhibits a sort of U-shaped trend. Let’s try to force convexity.
[23]:
pw = RobustPWRegression(objective="l1", degree=1, monotonic_trend="convex")
pw.fit(x, y, splits)
[23]:
RobustPWRegression(monotonic_trend='convex', objective='l1')
[24]:
report(x, y, pw, splits)
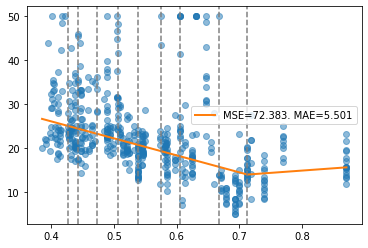
To reduce the mean squared error (MSE) and mean absolute error (MAE), we replace convex by valley.
[25]:
pw = RobustPWRegression(objective="l1", degree=1, monotonic_trend="valley")
pw.fit(x, y, splits)
[25]:
RobustPWRegression(monotonic_trend='valley', objective='l1')
[26]:
report(x, y, pw, splits)
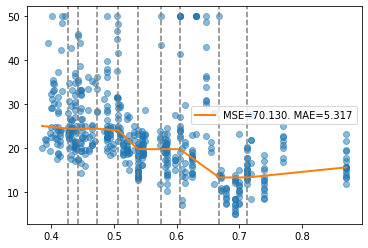
Note that, for degree >= 2 and convex/concave monotonicity, the monotonicity constraint is only satisfied at each bin individually. For this case, selecting \(l_1\)-norm, we notice that the LP solver HIGHS performs better.
[27]:
pw = RobustPWRegression(objective="l1", degree=3, continuous_deriv=False,
monotonic_trend="convex", solver="highs")
pw.fit(x, y, splits)
[27]:
RobustPWRegression(continuous_deriv=False, degree=3, monotonic_trend='convex',
objective='l1', solver='highs')
[28]:
report(x, y, pw, splits)
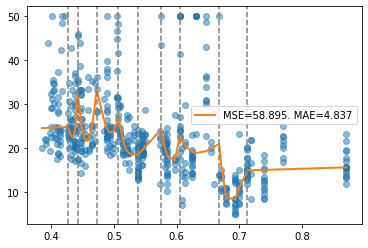
For those cases, we recommend avoiding splits points and fit a polynomial directly or constraining continuous derivatives at the split point.
[29]:
pw = RobustPWRegression(objective="l1", degree=3, monotonic_trend="convex")
pw.fit(x, y, splits=None)
[29]:
RobustPWRegression(degree=3, monotonic_trend='convex', objective='l1')
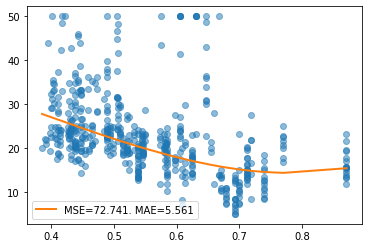
[30]:
report(x, y, pw, splits=[])
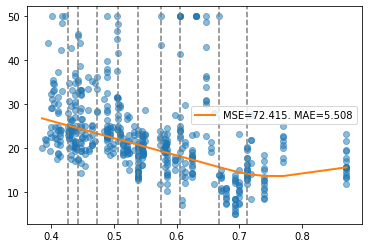
[31]:
pw = RobustPWRegression(objective="l1", degree=3, continuous_deriv=True,
monotonic_trend="convex", solver="highs")
pw.fit(x, y, splits)
[31]:
RobustPWRegression(degree=3, monotonic_trend='convex', objective='l1',
solver='highs')
[32]:
report(x, y, pw, splits)
Advanced¶
For the advanced section, we load a larger dataset.
[33]:
data = fetch_california_housing()
df = pd.DataFrame(data.data, columns=data.feature_names)
df["target"] = data.target
x = df["MedInc"].values
y = df["target"].values
[34]:
est = KBinsDiscretizer(n_bins=15, strategy="quantile")
est.fit(x.reshape(-1, 1), y)
splits = est.bin_edges_[0][1:-1]
If the trend of the relationship with the target is unclear, use the default piecewise regression.
[35]:
pw = RobustPWRegression(solver="osqp")
pw.fit(x, y, splits)
[35]:
RobustPWRegression(solver='osqp')
[36]:
report(x, y, pw, splits)
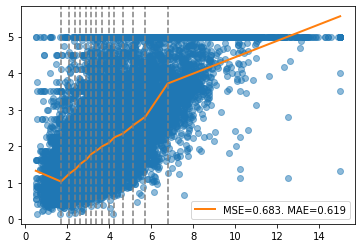
We observe an ascending monotonic trend. Let’s impose ascending monotonicity and show the solver’s output.
[37]:
pw = RobustPWRegression(objective="l2", monotonic_trend="ascending", verbose=True)
pw.fit(x, y, splits)
===============================================================================
CVXPY
v1.2.1
===============================================================================
(CVXPY) Dec 17 11:18:50 PM: Your problem has 30 variables, 2 constraints, and 0 parameters.
(CVXPY) Dec 17 11:18:50 PM: It is compliant with the following grammars: DCP, DQCP
(CVXPY) Dec 17 11:18:50 PM: (If you need to solve this problem multiple times, but with different data, consider using parameters.)
(CVXPY) Dec 17 11:18:50 PM: CVXPY will first compile your problem; then, it will invoke a numerical solver to obtain a solution.
-------------------------------------------------------------------------------
Compilation
-------------------------------------------------------------------------------
(CVXPY) Dec 17 11:18:50 PM: Compiling problem (target solver=OSQP).
(CVXPY) Dec 17 11:18:50 PM: Reduction chain: CvxAttr2Constr -> Qp2SymbolicQp -> QpMatrixStuffing -> OSQP
(CVXPY) Dec 17 11:18:50 PM: Applying reduction CvxAttr2Constr
(CVXPY) Dec 17 11:18:50 PM: Applying reduction Qp2SymbolicQp
(CVXPY) Dec 17 11:18:50 PM: Applying reduction QpMatrixStuffing
(CVXPY) Dec 17 11:18:50 PM: Applying reduction OSQP
(CVXPY) Dec 17 11:18:50 PM: Finished problem compilation (took 4.049e-02 seconds).
-------------------------------------------------------------------------------
Numerical solver
-------------------------------------------------------------------------------
(CVXPY) Dec 17 11:18:50 PM: Invoking solver OSQP to obtain a solution.
-----------------------------------------------------------------
OSQP v0.6.0 - Operator Splitting QP Solver
(c) Bartolomeo Stellato, Goran Banjac
University of Oxford - Stanford University 2019
-----------------------------------------------------------------
problem: variables n = 30, constraints m = 44
nnz(P) + nnz(A) = 116
settings: linear system solver = qdldl,
eps_abs = 1.0e-05, eps_rel = 1.0e-05,
eps_prim_inf = 1.0e-04, eps_dual_inf = 1.0e-04,
rho = 1.00e-01 (adaptive),
sigma = 1.00e-06, alpha = 1.60, max_iter = 10000
check_termination: on (interval 25),
scaling: on, scaled_termination: off
warm start: on, polish: on, time_limit: off
iter objective pri res dua res rho time
1 -6.0212e+04 2.79e-03 4.32e+04 1.00e-01 2.49e-04s
150 -1.0169e+05 4.63e-06 1.31e-01 3.16e-04 8.46e-04s
plsh -1.0169e+05 1.10e-13 2.39e-04 -------- 4.47e-03s
status: solved
solution polish: successful
number of iterations: 150
optimal objective: -101686.7435
run time: 4.47e-03s
optimal rho estimate: 4.64e-04
-------------------------------------------------------------------------------
Summary
-------------------------------------------------------------------------------
(CVXPY) Dec 17 11:18:50 PM: Problem status: optimal
(CVXPY) Dec 17 11:18:50 PM: Optimal value: -1.017e+05
(CVXPY) Dec 17 11:18:50 PM: Compilation took 4.049e-02 seconds
(CVXPY) Dec 17 11:18:50 PM: Solver (including time spent in interface) took 1.952e-02 seconds
[37]:
RobustPWRegression(monotonic_trend='ascending', verbose=True)
The Quadratic Programming (QP) solver OSQP (solver="osqp") is chosen. The option solver="auto" selects the most appropriate solver given the user’s parameters. We can switch to the ECOS solver using solver="ecos".
[38]:
pw = RobustPWRegression(objective="l2", monotonic_trend="ascending", solver="ecos",
verbose=True)
pw.fit(x, y, splits)
===============================================================================
CVXPY
v1.2.1
===============================================================================
(CVXPY) Dec 17 11:18:58 PM: Your problem has 30 variables, 2 constraints, and 0 parameters.
(CVXPY) Dec 17 11:18:58 PM: It is compliant with the following grammars: DCP, DQCP
(CVXPY) Dec 17 11:18:58 PM: (If you need to solve this problem multiple times, but with different data, consider using parameters.)
(CVXPY) Dec 17 11:18:58 PM: CVXPY will first compile your problem; then, it will invoke a numerical solver to obtain a solution.
-------------------------------------------------------------------------------
Compilation
-------------------------------------------------------------------------------
(CVXPY) Dec 17 11:18:58 PM: Compiling problem (target solver=ECOS).
(CVXPY) Dec 17 11:18:58 PM: Reduction chain: Dcp2Cone -> CvxAttr2Constr -> ConeMatrixStuffing -> ECOS
(CVXPY) Dec 17 11:18:58 PM: Applying reduction Dcp2Cone
(CVXPY) Dec 17 11:18:58 PM: Applying reduction CvxAttr2Constr
(CVXPY) Dec 17 11:18:58 PM: Applying reduction ConeMatrixStuffing
(CVXPY) Dec 17 11:18:58 PM: Applying reduction ECOS
(CVXPY) Dec 17 11:18:58 PM: Finished problem compilation (took 8.742e-02 seconds).
-------------------------------------------------------------------------------
Numerical solver
-------------------------------------------------------------------------------
(CVXPY) Dec 17 11:18:58 PM: Invoking solver ECOS to obtain a solution.
ECOS 2.0.7 - (C) embotech GmbH, Zurich Switzerland, 2012-15. Web: www.embotech.com/ECOS
It pcost dcost gap pres dres k/t mu step sigma IR | BT
0 +0.000e+00 -0.000e+00 +1e+04 5e-01 3e-04 1e+00 4e+02 --- --- 1 1 - | - -
1 +1.850e+00 +1.884e+00 +2e+02 1e-02 6e-06 6e-02 7e+00 0.9795 1e-04 3 3 3 | 0 0
2 +9.096e+01 +9.134e+01 +3e+01 1e-03 5e-07 4e-01 9e-01 0.9522 5e-02 7 8 8 | 0 0
3 +1.183e+02 +1.183e+02 +9e-01 3e-05 1e-08 1e-02 3e-02 0.9808 1e-04 2 3 3 | 0 0
4 +1.187e+02 +1.187e+02 +2e-01 8e-06 2e-09 4e-03 6e-03 0.8242 5e-02 2 2 2 | 0 0
5 +1.188e+02 +1.188e+02 +5e-03 5e-07 7e-11 2e-04 2e-04 0.9789 1e-02 6 5 5 | 0 0
6 +1.188e+02 +1.188e+02 +4e-04 2e-07 6e-12 1e-05 1e-05 0.9204 3e-03 6 5 5 | 0 0
7 +1.188e+02 +1.188e+02 +3e-05 1e-07 4e-13 1e-06 1e-06 0.9844 5e-02 1 2 2 | 0 0
8 +1.188e+02 +1.188e+02 +6e-07 7e-09 4e-14 2e-08 2e-08 0.9890 5e-03 7 4 5 | 0 0
OPTIMAL (within feastol=7.0e-09, reltol=4.8e-09, abstol=5.7e-07).
Runtime: 0.172480 seconds.
-------------------------------------------------------------------------------
Summary
-------------------------------------------------------------------------------
(CVXPY) Dec 17 11:18:59 PM: Problem status: optimal
(CVXPY) Dec 17 11:18:59 PM: Optimal value: 1.188e+02
(CVXPY) Dec 17 11:18:59 PM: Compilation took 8.742e-02 seconds
(CVXPY) Dec 17 11:18:59 PM: Solver (including time spent in interface) took 1.749e-01 seconds
[38]:
RobustPWRegression(monotonic_trend='ascending', solver='ecos', verbose=True)
Note that ECOS is significantly slower for this problem. However, the Second Order Cone Programming (SOCP) solver ECOS is more versatile, handling all the objectives and regularizations options available. Additionally, is better suited for large problems occurring when bounds are imposed.
Regularization¶
A regularization term using \(l_1-\)norm (Lasso) \(l_2-\)norm (Ridge) can be added to the objective function.
[39]:
pw = RobustPWRegression(objective="huber", monotonic_trend="ascending",
degree=2, regularization="l1", verbose=True)
pw.fit(x, y, splits)
===============================================================================
CVXPY
v1.2.1
===============================================================================
(CVXPY) Dec 17 11:19:07 PM: Your problem has 45 variables, 2 constraints, and 0 parameters.
(CVXPY) Dec 17 11:19:07 PM: It is compliant with the following grammars: DCP, DQCP
(CVXPY) Dec 17 11:19:07 PM: (If you need to solve this problem multiple times, but with different data, consider using parameters.)
(CVXPY) Dec 17 11:19:07 PM: CVXPY will first compile your problem; then, it will invoke a numerical solver to obtain a solution.
-------------------------------------------------------------------------------
Compilation
-------------------------------------------------------------------------------
(CVXPY) Dec 17 11:19:07 PM: Compiling problem (target solver=ECOS).
(CVXPY) Dec 17 11:19:07 PM: Reduction chain: Dcp2Cone -> CvxAttr2Constr -> ConeMatrixStuffing -> ECOS
(CVXPY) Dec 17 11:19:07 PM: Applying reduction Dcp2Cone
(CVXPY) Dec 17 11:19:07 PM: Applying reduction CvxAttr2Constr
(CVXPY) Dec 17 11:19:07 PM: Applying reduction ConeMatrixStuffing
(CVXPY) Dec 17 11:19:08 PM: Applying reduction ECOS
(CVXPY) Dec 17 11:19:08 PM: Finished problem compilation (took 3.434e-01 seconds).
-------------------------------------------------------------------------------
Numerical solver
-------------------------------------------------------------------------------
(CVXPY) Dec 17 11:19:08 PM: Invoking solver ECOS to obtain a solution.
ECOS 2.0.7 - (C) embotech GmbH, Zurich Switzerland, 2012-15. Web: www.embotech.com/ECOS
It pcost dcost gap pres dres k/t mu step sigma IR | BT
0 +0.000e+00 -6.012e+03 +5e+05 8e-01 5e+00 1e+00 6e+00 --- --- 2 1 - | - -
1 +4.636e+02 -4.432e+03 +4e+05 7e-01 7e-01 2e+00 5e+00 0.2691 5e-01 2 1 1 | 0 0
2 +2.760e+03 +1.008e+03 +2e+05 4e-01 9e-02 1e+00 2e+00 0.7340 2e-01 1 1 1 | 0 0
3 +7.243e+03 +6.626e+03 +7e+04 2e-01 3e-02 5e-01 8e-01 0.7508 2e-01 2 1 1 | 0 0
4 +8.544e+03 +8.096e+03 +5e+04 1e-01 3e-02 4e-01 6e-01 0.4625 4e-01 2 2 2 | 0 0
5 +1.038e+04 +1.015e+04 +3e+04 6e-02 2e-02 2e-01 3e-01 0.5611 1e-01 2 1 2 | 0 0
6 +1.133e+04 +1.121e+04 +1e+04 3e-02 1e-02 1e-01 2e-01 0.5575 2e-01 2 1 2 | 0 0
7 +1.172e+04 +1.165e+04 +9e+03 2e-02 1e-02 6e-02 1e-01 0.6270 4e-01 1 1 2 | 0 0
8 +1.242e+04 +1.240e+04 +2e+03 6e-03 4e-03 1e-02 3e-02 0.8201 9e-02 2 2 2 | 0 0
9 +1.252e+04 +1.250e+04 +1e+03 3e-03 3e-03 8e-03 2e-02 0.4706 2e-01 1 1 2 | 0 0
10 +1.259e+04 +1.259e+04 +7e+02 2e-03 1e-03 4e-03 9e-03 0.6524 2e-01 2 2 1 | 0 0
11 +1.259e+04 +1.259e+04 +7e+02 2e-03 1e-03 4e-03 9e-03 0.1773 8e-01 1 1 2 | 0 0
12 +1.262e+04 +1.262e+04 +5e+02 1e-03 1e-03 3e-03 6e-03 0.3122 4e-02 2 1 1 | 0 0
13 +1.265e+04 +1.265e+04 +2e+02 6e-04 5e-04 1e-03 3e-03 0.9890 5e-01 1 2 1 | 0 0
14 +1.266e+04 +1.266e+04 +2e+02 4e-04 4e-04 9e-04 2e-03 0.3928 4e-01 1 1 1 | 0 0
15 +1.267e+04 +1.267e+04 +1e+02 3e-04 3e-04 6e-04 1e-03 0.9890 7e-01 2 1 1 | 0 0
16 +1.268e+04 +1.268e+04 +1e+01 3e-05 3e-05 7e-05 2e-04 0.9890 1e-01 1 1 1 | 0 0
17 +1.268e+04 +1.268e+04 +2e+00 5e-06 5e-06 1e-05 3e-05 0.8704 2e-02 2 1 1 | 0 0
18 +1.268e+04 +1.268e+04 +7e-01 2e-06 1e-06 3e-06 8e-06 0.9890 3e-01 2 1 1 | 0 0
19 +1.268e+04 +1.268e+04 +8e-02 2e-07 2e-07 4e-07 1e-06 0.8933 1e-02 2 1 1 | 0 0
20 +1.268e+04 +1.268e+04 +1e-02 3e-08 3e-08 7e-08 2e-07 0.9890 2e-01 2 1 1 | 0 0
21 +1.268e+04 +1.268e+04 +3e-04 7e-10 6e-10 1e-09 3e-09 0.9809 6e-04 2 1 1 | 0 0
22 +1.268e+04 +1.268e+04 +3e-06 2e-10 6e-12 2e-11 4e-11 0.9890 1e-04 2 1 1 | 0 0
OPTIMAL (within feastol=1.6e-10, reltol=2.5e-10, abstol=3.1e-06).
Runtime: 3.229647 seconds.
-------------------------------------------------------------------------------
Summary
-------------------------------------------------------------------------------
(CVXPY) Dec 17 11:19:11 PM: Problem status: optimal
(CVXPY) Dec 17 11:19:11 PM: Optimal value: 1.268e+04
(CVXPY) Dec 17 11:19:11 PM: Compilation took 3.434e-01 seconds
(CVXPY) Dec 17 11:19:11 PM: Solver (including time spent in interface) took 3.243e+00 seconds
[39]:
RobustPWRegression(degree=2, monotonic_trend='ascending', objective='huber',
regularization='l1', verbose=True)
[40]:
report(x, y, pw, splits)
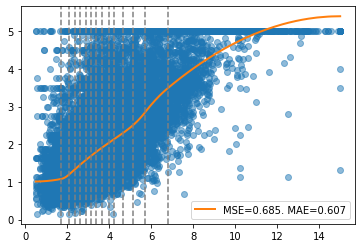
[41]:
pw = RobustPWRegression(objective="l2", monotonic_trend="ascending",
regularization="l2", verbose=True)
pw.fit(x, y, splits)
===============================================================================
CVXPY
v1.2.1
===============================================================================
(CVXPY) Dec 17 11:19:17 PM: Your problem has 30 variables, 2 constraints, and 0 parameters.
(CVXPY) Dec 17 11:19:17 PM: It is compliant with the following grammars: DCP, DQCP
(CVXPY) Dec 17 11:19:17 PM: (If you need to solve this problem multiple times, but with different data, consider using parameters.)
(CVXPY) Dec 17 11:19:17 PM: CVXPY will first compile your problem; then, it will invoke a numerical solver to obtain a solution.
-------------------------------------------------------------------------------
Compilation
-------------------------------------------------------------------------------
(CVXPY) Dec 17 11:19:17 PM: Compiling problem (target solver=ECOS).
(CVXPY) Dec 17 11:19:17 PM: Reduction chain: Dcp2Cone -> CvxAttr2Constr -> ConeMatrixStuffing -> ECOS
(CVXPY) Dec 17 11:19:17 PM: Applying reduction Dcp2Cone
(CVXPY) Dec 17 11:19:17 PM: Applying reduction CvxAttr2Constr
(CVXPY) Dec 17 11:19:17 PM: Applying reduction ConeMatrixStuffing
(CVXPY) Dec 17 11:19:17 PM: Applying reduction ECOS
(CVXPY) Dec 17 11:19:17 PM: Finished problem compilation (took 7.603e-02 seconds).
-------------------------------------------------------------------------------
Numerical solver
-------------------------------------------------------------------------------
(CVXPY) Dec 17 11:19:17 PM: Invoking solver ECOS to obtain a solution.
ECOS 2.0.7 - (C) embotech GmbH, Zurich Switzerland, 2012-15. Web: www.embotech.com/ECOS
It pcost dcost gap pres dres k/t mu step sigma IR | BT
0 +0.000e+00 -0.000e+00 +1e+04 9e-01 3e-04 1e+00 4e+02 --- --- 1 1 - | - -
1 +1.166e+00 +1.320e+00 +1e+03 7e-02 3e-05 3e-01 4e+01 0.8967 5e-04 3 3 3 | 0 0
2 -3.517e+00 -2.508e+00 +9e+02 4e-02 2e-05 1e+00 3e+01 0.2528 1e-01 4 5 5 | 0 0
3 -1.504e+01 -1.024e+01 +7e+02 1e-02 2e-05 5e+00 2e+01 0.3347 4e-01 5 5 5 | 0 0
4 +3.145e+01 +3.210e+01 +9e+01 6e-03 2e-06 7e-01 3e+00 0.8796 3e-03 5 5 5 | 0 0
5 +1.099e+02 +1.101e+02 +1e+01 8e-04 2e-07 2e-01 3e-01 0.9227 3e-02 3 3 3 | 0 0
6 +1.201e+02 +1.202e+02 +2e+00 1e-04 4e-08 7e-02 5e-02 0.9682 1e-01 2 2 2 | 0 0
7 +1.212e+02 +1.213e+02 +5e-01 5e-05 1e-08 2e-02 2e-02 0.7164 4e-02 2 2 2 | 0 0
8 +1.217e+02 +1.217e+02 +1e-01 1e-05 4e-09 7e-03 4e-03 0.8770 2e-01 9 9 9 | 0 0
9 +1.218e+02 +1.218e+02 +2e-02 3e-06 6e-10 1e-03 7e-04 0.8365 2e-02 1 2 2 | 0 0
10 +1.218e+02 +1.218e+02 +6e-03 8e-07 2e-10 3e-04 2e-04 0.7269 2e-02 7 6 7 | 0 0
11 +1.218e+02 +1.218e+02 +2e-03 3e-07 6e-11 1e-04 6e-05 0.8013 1e-01 6 5 5 | 0 0
12 +1.218e+02 +1.218e+02 +3e-04 8e-08 9e-12 2e-05 1e-05 0.8615 2e-02 1 2 2 | 0 0
13 +1.218e+02 +1.218e+02 +2e-05 2e-08 6e-13 1e-06 7e-07 0.9484 2e-02 5 4 4 | 0 0
14 +1.218e+02 +1.218e+02 +3e-06 6e-09 9e-14 2e-07 1e-07 0.8664 2e-02 1 2 2 | 0 0
15 +1.218e+02 +1.218e+02 +6e-07 3e-09 2e-14 3e-08 2e-08 0.8299 3e-02 9 6 6 | 0 0
OPTIMAL (within feastol=3.0e-09, reltol=5.2e-09, abstol=6.3e-07).
Runtime: 0.329856 seconds.
-------------------------------------------------------------------------------
Summary
-------------------------------------------------------------------------------
(CVXPY) Dec 17 11:19:17 PM: Problem status: optimal
(CVXPY) Dec 17 11:19:17 PM: Optimal value: 1.218e+02
(CVXPY) Dec 17 11:19:17 PM: Compilation took 7.603e-02 seconds
(CVXPY) Dec 17 11:19:17 PM: Solver (including time spent in interface) took 3.304e-01 seconds
[41]:
RobustPWRegression(monotonic_trend='ascending', regularization='l2',
verbose=True)
[42]:
report(x, y, pw, splits)
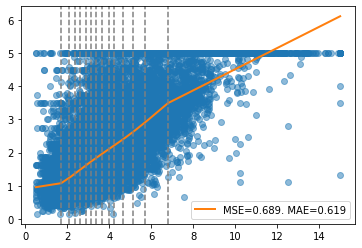
Increasing the regularization term using parameters reg_l1 and reg_l2 will produce a smoother piecewise regression.
Lower and upper bound¶
In some circumstances, it is required to impose a lower or upper limit to the prediction. For example, if we are predicting house prices, we might need to fix a minimum and maximum price. Parameters lb and ub in method fit impose these constraints.
[43]:
pw = RobustPWRegression(objective="l2", monotonic_trend="ascending", verbose=True)
pw.fit(x, y, splits, lb=1, ub=5)
===============================================================================
CVXPY
v1.2.1
===============================================================================
(CVXPY) Dec 17 11:19:31 PM: Your problem has 30 variables, 4 constraints, and 0 parameters.
(CVXPY) Dec 17 11:19:31 PM: It is compliant with the following grammars: DCP, DQCP
(CVXPY) Dec 17 11:19:31 PM: (If you need to solve this problem multiple times, but with different data, consider using parameters.)
(CVXPY) Dec 17 11:19:31 PM: CVXPY will first compile your problem; then, it will invoke a numerical solver to obtain a solution.
-------------------------------------------------------------------------------
Compilation
-------------------------------------------------------------------------------
(CVXPY) Dec 17 11:19:31 PM: Compiling problem (target solver=ECOS).
(CVXPY) Dec 17 11:19:31 PM: Reduction chain: Dcp2Cone -> CvxAttr2Constr -> ConeMatrixStuffing -> ECOS
(CVXPY) Dec 17 11:19:31 PM: Applying reduction Dcp2Cone
(CVXPY) Dec 17 11:19:31 PM: Applying reduction CvxAttr2Constr
(CVXPY) Dec 17 11:19:31 PM: Applying reduction ConeMatrixStuffing
(CVXPY) Dec 17 11:19:31 PM: Applying reduction ECOS
(CVXPY) Dec 17 11:19:31 PM: Finished problem compilation (took 7.374e-02 seconds).
-------------------------------------------------------------------------------
Numerical solver
-------------------------------------------------------------------------------
(CVXPY) Dec 17 11:19:31 PM: Invoking solver ECOS to obtain a solution.
ECOS 2.0.7 - (C) embotech GmbH, Zurich Switzerland, 2012-15. Web: www.embotech.com/ECOS
It pcost dcost gap pres dres k/t mu step sigma IR | BT
0 +0.000e+00 -5.033e+00 +1e+04 3e-01 3e-04 1e+00 3e+02 --- --- 1 1 - | - -
1 -2.286e+00 -3.017e+00 +4e+03 1e-01 9e-05 1e+00 1e+02 0.6852 4e-03 3 3 3 | 0 0
2 +7.203e+00 +7.182e+00 +1e+02 6e-03 4e-06 6e-02 4e+00 0.9592 1e-04 4 3 3 | 0 0
3 +8.125e+01 +8.142e+01 +5e+01 2e-03 1e-06 2e-01 1e+00 0.7076 6e-02 8 9 9 | 0 0
4 +1.173e+02 +1.173e+02 +2e+00 5e-05 2e-08 1e-02 6e-02 0.9799 8e-04 8 9 9 | 0 0
5 +1.189e+02 +1.189e+02 +8e-02 2e-06 9e-10 5e-04 2e-03 0.9613 1e-03 2 2 2 | 0 0
6 +1.190e+02 +1.190e+02 +2e-03 1e-07 2e-11 1e-05 4e-05 0.9808 1e-04 5 8 9 | 0 0
7 +1.190e+02 +1.190e+02 +6e-05 2e-08 7e-13 4e-07 2e-06 0.9628 5e-04 4 6 6 | 0 0
8 +1.190e+02 +1.190e+02 +2e-06 5e-09 5e-14 1e-08 4e-08 0.9728 7e-04 3 4 4 | 0 0
9 +1.190e+02 +1.190e+02 +2e-07 5e-09 9e-15 3e-09 7e-09 0.8840 3e-02 3 6 6 | 0 0
OPTIMAL (within feastol=5.0e-09, reltol=2.0e-09, abstol=2.3e-07).
Runtime: 0.217148 seconds.
-------------------------------------------------------------------------------
Summary
-------------------------------------------------------------------------------
(CVXPY) Dec 17 11:19:31 PM: Problem status: optimal
(CVXPY) Dec 17 11:19:31 PM: Optimal value: 1.190e+02
(CVXPY) Dec 17 11:19:31 PM: Compilation took 7.374e-02 seconds
(CVXPY) Dec 17 11:19:31 PM: Solver (including time spent in interface) took 2.187e-01 seconds
[43]:
RobustPWRegression(monotonic_trend='ascending', verbose=True)
[44]:
report(x, y, pw, splits)
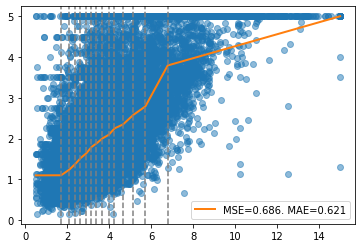
As previously mentioned, ECOS is more adequate when bounds are active. OSQP requires more than 11 seconds to solve this problem and returns an inacurate solution. For large scale problems, a general alternative is the solver SCS.
[45]:
pw = RobustPWRegression(objective="l2", solver="scs", monotonic_trend="ascending",
verbose=True)
pw.fit(x, y, splits, lb=1, ub=5)
===============================================================================
CVXPY
v1.2.1
===============================================================================
(CVXPY) Dec 17 11:19:49 PM: Your problem has 30 variables, 4 constraints, and 0 parameters.
(CVXPY) Dec 17 11:19:49 PM: It is compliant with the following grammars: DCP, DQCP
(CVXPY) Dec 17 11:19:49 PM: (If you need to solve this problem multiple times, but with different data, consider using parameters.)
(CVXPY) Dec 17 11:19:49 PM: CVXPY will first compile your problem; then, it will invoke a numerical solver to obtain a solution.
-------------------------------------------------------------------------------
Compilation
-------------------------------------------------------------------------------
(CVXPY) Dec 17 11:19:49 PM: Compiling problem (target solver=SCS).
(CVXPY) Dec 17 11:19:49 PM: Reduction chain: Dcp2Cone -> CvxAttr2Constr -> ConeMatrixStuffing -> SCS
(CVXPY) Dec 17 11:19:49 PM: Applying reduction Dcp2Cone
(CVXPY) Dec 17 11:19:49 PM: Applying reduction CvxAttr2Constr
(CVXPY) Dec 17 11:19:49 PM: Applying reduction ConeMatrixStuffing
(CVXPY) Dec 17 11:19:49 PM: Applying reduction SCS
(CVXPY) Dec 17 11:19:49 PM: Finished problem compilation (took 6.646e-02 seconds).
-------------------------------------------------------------------------------
Numerical solver
-------------------------------------------------------------------------------
(CVXPY) Dec 17 11:19:49 PM: Invoking solver SCS to obtain a solution.
----------------------------------------------------------------------------
SCS v2.1.2 - Splitting Conic Solver
(c) Brendan O'Donoghue, Stanford University, 2012
----------------------------------------------------------------------------
Lin-sys: sparse-direct, nnz in A = 41360
eps = 1.00e-04, alpha = 1.50, max_iters = 5000, normalize = 1, scale = 1.00
acceleration_lookback = 10, rho_x = 1.00e-03
Variables n = 31, constraints m = 20689
Cones: primal zero / dual free vars: 14
linear vars: 34
soc vars: 20641, soc blks: 1
Setup time: 6.78e-02s
----------------------------------------------------------------------------
Iter | pri res | dua res | rel gap | pri obj | dua obj | kap/tau | time (s)
----------------------------------------------------------------------------
0| 1.41e+19 6.72e+19 1.00e+00 -1.84e+20 1.26e+22 1.15e+22 2.54e-02
100| 1.79e-07 3.16e-04 6.03e-07 1.19e+02 1.19e+02 3.58e-16 4.52e-01
120| 8.65e-08 5.21e-06 3.95e-08 1.19e+02 1.19e+02 2.12e-16 5.43e-01
----------------------------------------------------------------------------
Status: Solved
Timing: Solve time: 5.44e-01s
Lin-sys: nnz in L factor: 62122, avg solve time: 3.14e-04s
Cones: avg projection time: 4.04e-05s
Acceleration: avg step time: 3.43e-03s
----------------------------------------------------------------------------
Error metrics:
dist(s, K) = 4.5629e-16, dist(y, K*) = 0.0000e+00, s'y/|s||y| = 1.6437e-15
primal res: |Ax + s - b|_2 / (1 + |b|_2) = 8.6547e-08
dual res: |A'y + c|_2 / (1 + |c|_2) = 5.2132e-06
rel gap: |c'x + b'y| / (1 + |c'x| + |b'y|) = 3.9539e-08
----------------------------------------------------------------------------
c'x = 118.9762, -b'y = 118.9762
============================================================================
-------------------------------------------------------------------------------
Summary
-------------------------------------------------------------------------------
(CVXPY) Dec 17 11:19:49 PM: Problem status: optimal
(CVXPY) Dec 17 11:19:49 PM: Optimal value: 1.190e+02
(CVXPY) Dec 17 11:19:49 PM: Compilation took 6.646e-02 seconds
(CVXPY) Dec 17 11:19:49 PM: Solver (including time spent in interface) took 6.393e-01 seconds
[45]:
RobustPWRegression(monotonic_trend='ascending', solver='scs', verbose=True)