Tutorial: FICO Explainable Machine Learning Challenge¶
In this tutorial, we use the dataset form the FICO Explainable Machine Learning Challenge: https://community.fico.com/s/explainable-machine-learning-challenge. The goal is to create a pipeline by combining a binning process and logistic regression to obtain an explainable model and compare it against a black-box model using Gradient Boosting Tree (GBT) as an estimator.
[1]:
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
[2]:
from optbinning import BinningProcess
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.metrics import classification_report
from sklearn.metrics import auc, roc_auc_score, roc_curve
from sklearn.model_selection import train_test_split
from sklearn.pipeline import Pipeline
Download the dataset from the link above and load it.
[3]:
df = pd.read_csv("data/FICO_challenge/heloc_dataset_v1.csv", sep=",")
[4]:
variable_names = list(df.columns[1:])
[5]:
X = df[variable_names].values
Transform the categorical dichotomic target variable into numerical.
[6]:
y = df.RiskPerformance.values
mask = y == "Bad"
y[mask] = 1
y[~mask] = 0
y = y.astype(int)
Modeling¶
The data dictionary of this challenge includes three special values/codes:
-9 No Bureau Record or No Investigation
-8 No Usable/Valid Trades or Inquiries
-7 Condition not Met (e.g. No Inquiries, No Delinquencies)
[7]:
special_codes = [-9, -8, -7]
This challenge imposes monotonicity constraints with respect to the probability of a bad target for many of the variables. We apply these rules by passing the following dictionary of parameters for these variables involved.
[8]:
binning_fit_params = {
"ExternalRiskEstimate": {"monotonic_trend": "descending"},
"MSinceOldestTradeOpen": {"monotonic_trend": "descending"},
"MSinceMostRecentTradeOpen": {"monotonic_trend": "descending"},
"AverageMInFile": {"monotonic_trend": "descending"},
"NumSatisfactoryTrades": {"monotonic_trend": "descending"},
"NumTrades60Ever2DerogPubRec": {"monotonic_trend": "ascending"},
"NumTrades90Ever2DerogPubRec": {"monotonic_trend": "ascending"},
"PercentTradesNeverDelq": {"monotonic_trend": "descending"},
"MSinceMostRecentDelq": {"monotonic_trend": "descending"},
"NumTradesOpeninLast12M": {"monotonic_trend": "ascending"},
"MSinceMostRecentInqexcl7days": {"monotonic_trend": "descending"},
"NumInqLast6M": {"monotonic_trend": "ascending"},
"NumInqLast6Mexcl7days": {"monotonic_trend": "ascending"},
"NetFractionRevolvingBurden": {"monotonic_trend": "ascending"},
"NetFractionInstallBurden": {"monotonic_trend": "ascending"},
"NumBank2NatlTradesWHighUtilization": {"monotonic_trend": "ascending"}
}
Instantiate a BinningProcess object class with variable names, special codes and dictionary of binning parameters. Create a explainable model pipeline and a black-blox pipeline.
[9]:
binning_process = BinningProcess(variable_names, special_codes=special_codes,
binning_fit_params=binning_fit_params)
[10]:
clf1 = Pipeline(steps=[('binning_process', binning_process),
('classifier', LogisticRegression(solver="lbfgs"))])
clf2 = LogisticRegression(solver="lbfgs")
clf3 = GradientBoostingClassifier()
Split dataset into train and test. Fit pipelines with training data, then generate classification reports to show the main classification metrics.
[11]:
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
[12]:
clf1.fit(X_train, y_train)
/home/gui/projects/github/top/optbinning/optbinning/binning/transformations.py:38: RuntimeWarning: invalid value encountered in log
return np.log((1. / event_rate - 1) * n_event / n_nonevent)
[12]:
Pipeline(steps=[('binning_process',
BinningProcess(binning_fit_params={'AverageMInFile': {'monotonic_trend': 'descending'},
'ExternalRiskEstimate': {'monotonic_trend': 'descending'},
'MSinceMostRecentDelq': {'monotonic_trend': 'descending'},
'MSinceMostRecentInqexcl7days': {'monotonic_trend': 'descending'},
'MSinceMostRecentTradeOpen': {'monotonic_trend': 'descen...
'MaxDelqEver', 'NumTotalTrades',
'NumTradesOpeninLast12M',
'PercentInstallTrades',
'MSinceMostRecentInqexcl7days',
'NumInqLast6M',
'NumInqLast6Mexcl7days',
'NetFractionRevolvingBurden',
'NetFractionInstallBurden',
'NumRevolvingTradesWBalance',
'NumInstallTradesWBalance',
'NumBank2NatlTradesWHighUtilization',
'PercentTradesWBalance'])),
('classifier', LogisticRegression())])
[13]:
clf2.fit(X_train, y_train)
/home/gui/anaconda3/lib/python3.7/site-packages/sklearn/linear_model/_logistic.py:818: ConvergenceWarning: lbfgs failed to converge (status=1):
STOP: TOTAL NO. of ITERATIONS REACHED LIMIT.
Increase the number of iterations (max_iter) or scale the data as shown in:
https://scikit-learn.org/stable/modules/preprocessing.html
Please also refer to the documentation for alternative solver options:
https://scikit-learn.org/stable/modules/linear_model.html#logistic-regression
extra_warning_msg=_LOGISTIC_SOLVER_CONVERGENCE_MSG,
[13]:
LogisticRegression()
[14]:
clf3.fit(X_train, y_train)
[14]:
GradientBoostingClassifier()
[15]:
y_pred = clf1.predict(X_test)
print(classification_report(y_test, y_pred))
precision recall f1-score support
0 0.70 0.66 0.68 1004
1 0.70 0.74 0.72 1088
accuracy 0.70 2092
macro avg 0.70 0.70 0.70 2092
weighted avg 0.70 0.70 0.70 2092
/home/gui/projects/github/top/optbinning/optbinning/binning/transformations.py:38: RuntimeWarning: invalid value encountered in log
return np.log((1. / event_rate - 1) * n_event / n_nonevent)
[16]:
y_pred = clf2.predict(X_test)
print(classification_report(y_test, y_pred))
precision recall f1-score support
0 0.67 0.66 0.67 1004
1 0.69 0.70 0.70 1088
accuracy 0.68 2092
macro avg 0.68 0.68 0.68 2092
weighted avg 0.68 0.68 0.68 2092
[17]:
y_pred = clf3.predict(X_test)
print(classification_report(y_test, y_pred))
precision recall f1-score support
0 0.71 0.66 0.68 1004
1 0.70 0.75 0.73 1088
accuracy 0.71 2092
macro avg 0.71 0.70 0.70 2092
weighted avg 0.71 0.71 0.70 2092
Plot the Receiver Operating Characteristic (ROC) metric to evaluate and compare the classifiers’ prediction.
[18]:
probs = clf1.predict_proba(X_test)
preds = probs[:,1]
fpr1, tpr1, threshold = roc_curve(y_test, preds)
roc_auc1 = auc(fpr1, tpr1)
probs = clf2.predict_proba(X_test)
preds = probs[:,1]
fpr2, tpr2, threshold = roc_curve(y_test, preds)
roc_auc2 = auc(fpr2, tpr2)
probs = clf3.predict_proba(X_test)
preds = probs[:,1]
fpr3, tpr3, threshold = roc_curve(y_test, preds)
roc_auc3 = auc(fpr3, tpr3)
/home/gui/projects/github/top/optbinning/optbinning/binning/transformations.py:38: RuntimeWarning: invalid value encountered in log
return np.log((1. / event_rate - 1) * n_event / n_nonevent)
[19]:
plt.title('Receiver Operating Characteristic')
plt.plot(fpr1, tpr1, 'b', label='Binning+LR: AUC = {0:.2f}'.format(roc_auc1))
plt.plot(fpr2, tpr2, 'g', label='LR: AUC = {0:.2f}'.format(roc_auc2))
plt.plot(fpr3, tpr3, 'r', label='GBT: AUC = {0:.2f}'.format(roc_auc3))
plt.legend(loc='lower right')
plt.plot([0, 1], [0, 1],'k--')
plt.xlim([0, 1])
plt.ylim([0, 1])
plt.ylabel('True Positive Rate')
plt.xlabel('False Positive Rate')
plt.show()
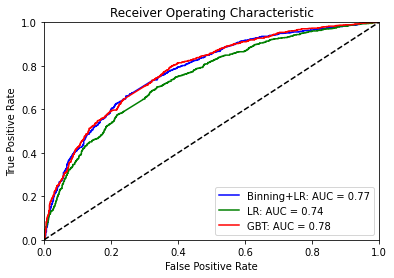
The plot above shows the increment in terms of model performance after binning when the logistic estimator is chosen. Furthermore, a previous binning process might reduce numerical instability issues, as confirmed when fitting the classifier clf2.
Binning process statistics¶
The binning process of the pipeline can be retrieved to show information about the problem and timing statistics.
[20]:
binning_process.information(print_level=2)
optbinning (Version 0.19.0)
Copyright (c) 2019-2024 Guillermo Navas-Palencia, Apache License 2.0
Begin options
max_n_prebins 20 * d
min_prebin_size 0.05 * d
min_n_bins no * d
max_n_bins no * d
min_bin_size no * d
max_bin_size no * d
max_pvalue no * d
max_pvalue_policy consecutive * d
selection_criteria no * d
fixed_variables no * d
categorical_variables no * d
special_codes yes * U
split_digits no * d
binning_fit_params yes * U
binning_transform_params no * d
verbose False * d
End options
Statistics
Number of records 8367
Number of variables 23
Target type binary
Number of numerical 23
Number of categorical 0
Number of selected 23
Time 2.3069 sec
The summary method returns basic statistics for each binned variable.
[21]:
binning_process.summary()
[21]:
| name | dtype | status | selected | n_bins | iv | js | gini | quality_score | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | ExternalRiskEstimate | numerical | OPTIMAL | True | 12 | 1.018368 | 0.116638 | 0.534387 | 0.031792 |
| 1 | MSinceOldestTradeOpen | numerical | OPTIMAL | True | 11 | 0.252786 | 0.030483 | 0.264740 | 0.027179 |
| 2 | MSinceMostRecentTradeOpen | numerical | OPTIMAL | True | 6 | 0.019086 | 0.002377 | 0.065597 | 0.000556 |
| 3 | AverageMInFile | numerical | OPTIMAL | True | 10 | 0.319379 | 0.038458 | 0.304157 | 0.128082 |
| 4 | NumSatisfactoryTrades | numerical | OPTIMAL | True | 10 | 0.126726 | 0.015424 | 0.180888 | 0.001210 |
| 5 | NumTrades60Ever2DerogPubRec | numerical | OPTIMAL | True | 4 | 0.178710 | 0.021915 | 0.200184 | 0.201631 |
| 6 | NumTrades90Ever2DerogPubRec | numerical | OPTIMAL | True | 3 | 0.133485 | 0.016301 | 0.155193 | 0.286527 |
| 7 | PercentTradesNeverDelq | numerical | OPTIMAL | True | 8 | 0.377803 | 0.045428 | 0.316946 | 0.101421 |
| 8 | MSinceMostRecentDelq | numerical | OPTIMAL | True | 7 | 0.289526 | 0.035246 | 0.272229 | 0.239494 |
| 9 | MaxDelq2PublicRecLast12M | numerical | OPTIMAL | True | 3 | 0.330280 | 0.040250 | 0.301670 | 0.833712 |
| 10 | MaxDelqEver | numerical | OPTIMAL | True | 4 | 0.236098 | 0.029129 | 0.257314 | 0.667940 |
| 11 | NumTotalTrades | numerical | OPTIMAL | True | 8 | 0.064716 | 0.008027 | 0.138545 | 0.011755 |
| 12 | NumTradesOpeninLast12M | numerical | OPTIMAL | True | 6 | 0.023530 | 0.002936 | 0.083770 | 0.007932 |
| 13 | PercentInstallTrades | numerical | OPTIMAL | True | 8 | 0.098610 | 0.012107 | 0.159569 | 0.077405 |
| 14 | MSinceMostRecentInqexcl7days | numerical | OPTIMAL | True | 4 | 0.166538 | 0.020460 | 0.211639 | 0.531041 |
| 15 | NumInqLast6M | numerical | OPTIMAL | True | 4 | 0.089956 | 0.011127 | 0.159369 | 0.323780 |
| 16 | NumInqLast6Mexcl7days | numerical | OPTIMAL | True | 5 | 0.083992 | 0.010394 | 0.153641 | 0.036291 |
| 17 | NetFractionRevolvingBurden | numerical | OPTIMAL | True | 9 | 0.574686 | 0.068232 | 0.410605 | 0.343593 |
| 18 | NetFractionInstallBurden | numerical | OPTIMAL | True | 5 | 0.037879 | 0.004724 | 0.105916 | 0.053723 |
| 19 | NumRevolvingTradesWBalance | numerical | OPTIMAL | True | 7 | 0.093376 | 0.011578 | 0.162108 | 0.011291 |
| 20 | NumInstallTradesWBalance | numerical | OPTIMAL | True | 5 | 0.014121 | 0.001762 | 0.059437 | 0.010423 |
| 21 | NumBank2NatlTradesWHighUtilization | numerical | OPTIMAL | True | 5 | 0.334853 | 0.041017 | 0.308402 | 0.222126 |
| 22 | PercentTradesWBalance | numerical | OPTIMAL | True | 12 | 0.365412 | 0.044210 | 0.334112 | 0.018131 |
The get_binned_variable method serves to retrieve an optimal binning object, which can be analyzed in detail afterward.
[22]:
optb = binning_process.get_binned_variable("NumBank2NatlTradesWHighUtilization")
[23]:
optb.binning_table.build()
[23]:
| Bin | Count | Count (%) | Non-event | Event | Event rate | WoE | IV | JS | |
|---|---|---|---|---|---|---|---|---|---|
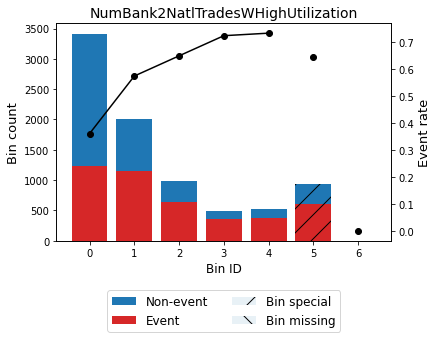
| 0 | (-inf, 0.50) | 3416 | 0.408271 | 2184 | 1232 | 0.360656 | 0.662217 | 0.175281 | 0.021518 |
| 1 | [0.50, 1.50) | 2015 | 0.240827 | 858 | 1157 | 0.574194 | -0.209284 | 0.010461 | 0.001305 |
| 2 | [1.50, 2.50) | 983 | 0.117485 | 345 | 638 | 0.649034 | -0.525096 | 0.031309 | 0.003869 |
| 3 | [2.50, 3.50) | 496 | 0.059281 | 137 | 359 | 0.723790 | -0.873644 | 0.041802 | 0.005065 |
| 4 | [3.50, inf) | 521 | 0.062268 | 139 | 382 | 0.733205 | -0.921249 | 0.048466 | 0.005853 |
| 5 | Special | 936 | 0.111868 | 333 | 603 | 0.644231 | -0.504077 | 0.027533 | 0.003406 |
| 6 | Missing | 0 | 0.000000 | 0 | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| Totals | 8367 | 1.000000 | 3996 | 4371 | 0.522409 | 0.334853 | 0.041017 |
[24]:
optb.binning_table.plot(metric="event_rate")
[25]:
optb.binning_table.analysis()
---------------------------------------------
OptimalBinning: Binary Binning Table Analysis
---------------------------------------------
General metrics
Gini index 0.30840174
IV (Jeffrey) 0.33485338
JS (Jensen-Shannon) 0.04101657
Hellinger 0.04143062
Triangular 0.16088993
KS 0.26468885
HHI 0.25839135
HHI (normalized) 0.13478991
Cramer's V 0.28612357
Quality score 0.22212566
Monotonic trend ascending
Significance tests
Bin A Bin B t-statistic p-value P[A > B] P[B > A]
0 1 234.556206 6.049946e-53 5.576352e-107 1.000000
1 2 15.402738 8.686234e-05 7.665294e-06 0.999992
2 3 8.386138 3.780934e-03 1.290940e-03 0.998709
3 4 0.113909 7.357368e-01 3.678894e-01 0.632111