Tutorial: optimal binning 2D with continuous target¶
To get us started, let’s load a well-known dataset from the UCI repository and transform the data into a pandas.DataFrame.
[1]:
import pandas as pd
from tests.datasets import load_boston
[2]:
data = load_boston()
df = pd.DataFrame(data.data, columns=data.feature_names)
We choose two variables to discretize and the continuous target.
[3]:
variable1 = "AGE"
variable2 = "INDUS"
x = df[variable1].values
y = df[variable2].values
z = data.target
Import and instantiate an ContinuousOptimalBinning2D object class. We pass the variable names (coordinates x and y), and a solver, in this case, we choose the constraint programming solver.
[4]:
from optbinning import ContinuousOptimalBinning2D
[5]:
optb = ContinuousOptimalBinning2D(name_x=variable1, name_y=variable2, solver="cp")
We fit the optimal binning object with arrays x, y, and z.
[6]:
optb.fit(x, y, z)
[6]:
ContinuousOptimalBinning2D(name_x='AGE', name_y='INDUS')
Similar to other OptBinning classes, you can inspect the attributes status and splits. In this case, the splits shown are actually the bins, but the splits name is used to maintain API homogeneity.
[7]:
optb.status
[7]:
'OPTIMAL'
[8]:
optb.splits
[8]:
([[-inf, 37.25],
[37.25, 76.25],
[76.25, 92.29999923706055],
[92.29999923706055, 98.25],
[98.25, inf],
[-inf, 37.25],
[37.25, 76.25],
[76.25, 92.29999923706055],
[92.29999923706055, 98.25],
[-inf, 37.25],
[37.25, 76.25],
[76.25, 98.25],
[98.25, inf],
[-inf, 37.25],
[37.25, 76.25],
[76.25, 92.29999923706055],
[92.29999923706055, 98.25],
[-inf, 76.25],
[76.25, 92.29999923706055],
[92.29999923706055, 98.25],
[98.25, inf]],
[[-inf, 3.9850000143051147],
[-inf, 3.9850000143051147],
[-inf, 3.9850000143051147],
[-inf, 3.9850000143051147],
[-inf, 6.080000162124634],
[3.9850000143051147, 6.080000162124634],
[3.9850000143051147, 6.080000162124634],
[3.9850000143051147, 6.080000162124634],
[3.9850000143051147, 6.080000162124634],
[6.080000162124634, 6.659999847412109],
[6.080000162124634, 6.659999847412109],
[6.080000162124634, 6.659999847412109],
[6.080000162124634, 16.570000171661377],
[6.659999847412109, 16.570000171661377],
[6.659999847412109, 16.570000171661377],
[6.659999847412109, 16.570000171661377],
[6.659999847412109, 16.570000171661377],
[16.570000171661377, inf],
[16.570000171661377, inf],
[16.570000171661377, inf],
[16.570000171661377, inf]])
The binning table¶
The binning table follows the same structure as the unidimensional binning, except for having two Bin columns, one for each variable (coordinate). The option show_bin_xy=True in method build combines both columns to obtain a single Bin column.
[9]:
optb.binning_table.build()
[9]:
| Bin x | Bin y | Count | Count (%) | Sum | Std | Mean | WoE | IV | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | (-inf, 37.25) | (-inf, 3.99) | 43 | 0.084980 | 1317.3 | 9.113544 | 30.634884 | 8.102077 | 0.688516 |
| 1 | [37.25, 76.25) | (-inf, 3.99) | 35 | 0.069170 | 1115.1 | 8.144242 | 31.860000 | 9.327194 | 0.645162 |
| 2 | [76.25, 92.30) | (-inf, 3.99) | 10 | 0.019763 | 370.6 | 8.343644 | 37.060000 | 14.527194 | 0.287099 |
| 3 | [92.30, 98.25) | (-inf, 3.99) | 2 | 0.003953 | 63.5 | 0.750000 | 31.750000 | 9.217194 | 0.036432 |
| 4 | [98.25, inf) | (-inf, 6.08) | 2 | 0.003953 | 66.1 | 2.950000 | 33.050000 | 10.517194 | 0.041570 |
| 5 | (-inf, 37.25) | [3.99, 6.08) | 27 | 0.053360 | 680.8 | 5.262706 | 25.214815 | 2.682008 | 0.143111 |
| 6 | [37.25, 76.25) | [3.99, 6.08) | 36 | 0.071146 | 773.6 | 2.676002 | 21.488889 | -1.043917 | 0.074271 |
| 7 | [76.25, 92.30) | [3.99, 6.08) | 4 | 0.007905 | 84.8 | 2.388514 | 21.200000 | -1.332806 | 0.010536 |
| 8 | [92.30, 98.25) | [3.99, 6.08) | 1 | 0.001976 | 16.0 | 0.000000 | 16.000000 | -6.532806 | 0.012911 |
| 9 | (-inf, 37.25) | [6.08, 6.66) | 7 | 0.013834 | 232.3 | 5.962365 | 33.185714 | 10.652908 | 0.147372 |
| 10 | [37.25, 76.25) | [6.08, 6.66) | 9 | 0.017787 | 286.0 | 8.119357 | 31.777778 | 9.244971 | 0.164436 |
| 11 | [76.25, 98.25) | [6.08, 6.66) | 10 | 0.019763 | 326.8 | 8.488086 | 32.680000 | 10.147194 | 0.200537 |
| 12 | [98.25, inf) | [6.08, 16.57) | 4 | 0.007905 | 65.5 | 2.246525 | 16.375000 | -6.157806 | 0.048678 |
| 13 | (-inf, 37.25) | [6.66, 16.57) | 23 | 0.045455 | 543.5 | 2.327610 | 23.630435 | 1.097628 | 0.049892 |
| 14 | [37.25, 76.25) | [6.66, 16.57) | 49 | 0.096838 | 1086.8 | 3.434815 | 22.179592 | -0.353214 | 0.034205 |
| 15 | [76.25, 92.30) | [6.66, 16.57) | 40 | 0.079051 | 777.0 | 3.359967 | 19.425000 | -3.107806 | 0.245676 |
| 16 | [92.30, 98.25) | [6.66, 16.57) | 15 | 0.029644 | 264.7 | 4.036478 | 17.646667 | -4.886140 | 0.144846 |
| 17 | (-inf, 76.25) | [16.57, inf) | 16 | 0.031621 | 324.4 | 4.472765 | 20.275000 | -2.257806 | 0.071393 |
| 18 | [76.25, 92.30) | [16.57, inf) | 50 | 0.098814 | 912.5 | 8.416228 | 18.250000 | -4.282806 | 0.423202 |
| 19 | [92.30, 98.25) | [16.57, inf) | 71 | 0.140316 | 1286.2 | 10.093278 | 18.115493 | -4.417313 | 0.619821 |
| 20 | [98.25, inf) | [16.57, inf) | 52 | 0.102767 | 808.1 | 8.662280 | 15.540385 | -6.992422 | 0.718589 |
| 21 | Special | Special | 0 | 0.000000 | 0.0 | 0.000000 | 0.000000 | -22.532806 | 0.000000 |
| 22 | Missing | Missing | 0 | 0.000000 | 0.0 | 0.000000 | 0.000000 | -22.532806 | 0.000000 |
| Totals | 506 | 1.000000 | 11401.6 | 22.532806 | 171.946019 | 4.808255 |
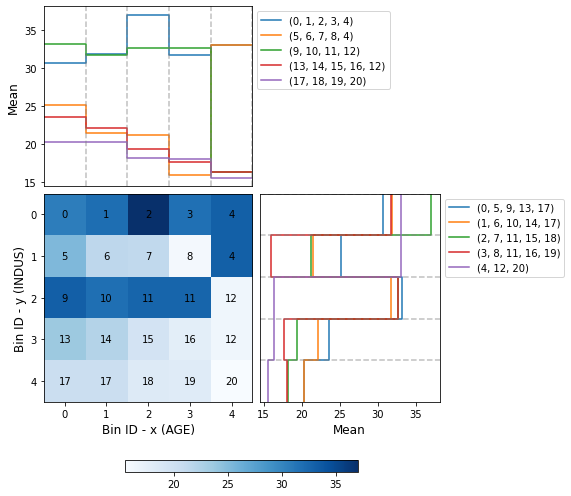
You can use the method plot to visualize the histogram 2D and mean curve. Note that the Bin ID corresponds to the binning table index. These are the key points to correctly interpret the plots belows:
Bins can only be rectangles. If a bin is composed by \(m\) squares, the Bin ID is shown \(m\) times.
The upper left plot shows the mean on the x-axis; the bin paths left-right.
The lower right plot shows the mean on the y-axis; the bin paths top-down.
[10]:
optb.binning_table.plot()
Mean transformation¶
Now that we have checked the binned data, we can transform our original data into mean values. You can check the correctness of the transformation using pandas value_counts method, for instance. Note that both x and y are required, and a single array is returned with the transformation.
[11]:
z_transform_mean = optb.transform(x, y, metric="mean")
pd.Series(z_transform_mean).value_counts()
[11]:
18.115493 71
15.540385 52
18.250000 50
22.179592 49
30.634884 43
19.425000 40
21.488889 36
31.860000 35
25.214815 27
23.630435 23
20.275000 16
17.646667 15
32.680000 10
37.060000 10
31.777778 9
33.185714 7
21.200000 4
16.375000 4
31.750000 2
33.050000 2
16.000000 1
dtype: int64
[12]:
z_transform_indices = optb.transform(x, y, metric="indices")
pd.Series(z_transform_indices).value_counts()
[12]:
19 71
20 52
18 50
14 49
0 43
15 40
6 36
1 35
5 27
13 23
17 16
16 15
11 10
2 10
10 9
9 7
7 4
12 4
4 2
3 2
8 1
dtype: int64
If metric="bins" the bin ids are combined.
[13]:
z_transform_bins = optb.transform(x, y, metric="bins")
pd.Series(z_transform_bins).value_counts()
[13]:
[92.30, 98.25) $\cup$ [16.57, inf) 71
[98.25, inf) $\cup$ [16.57, inf) 52
[76.25, 92.30) $\cup$ [16.57, inf) 50
[37.25, 76.25) $\cup$ [6.66, 16.57) 49
(-inf, 37.25) $\cup$ (-inf, 3.99) 43
[76.25, 92.30) $\cup$ [6.66, 16.57) 40
[37.25, 76.25) $\cup$ [3.99, 6.08) 36
[37.25, 76.25) $\cup$ (-inf, 3.99) 35
(-inf, 37.25) $\cup$ [3.99, 6.08) 27
(-inf, 37.25) $\cup$ [6.66, 16.57) 23
(-inf, 76.25) $\cup$ [16.57, inf) 16
[92.30, 98.25) $\cup$ [6.66, 16.57) 15
[76.25, 98.25) $\cup$ [6.08, 6.66) 10
[76.25, 92.30) $\cup$ (-inf, 3.99) 10
[37.25, 76.25) $\cup$ [6.08, 6.66) 9
(-inf, 37.25) $\cup$ [6.08, 6.66) 7
[98.25, inf) $\cup$ [6.08, 16.57) 4
[76.25, 92.30) $\cup$ [3.99, 6.08) 4
[98.25, inf) $\cup$ (-inf, 6.08) 2
[92.30, 98.25) $\cup$ (-inf, 3.99) 2
[92.30, 98.25) $\cup$ [3.99, 6.08) 1
dtype: int64
Binning table statistical analysis¶
The analysis method performs a statistical analysis of the binning table, computing the Information Value (IV), Weight of Evidence (WoE), and Herfindahl-Hirschman Index (HHI). The report is the same that the one for unidimensional binning with a continuous target. The main difference is that the significant tests for each bin are performed with respect to all its linked bins.
[14]:
optb.binning_table.analysis()
----------------------------------------------------
OptimalBinning: Continuous Binning Table 2D Analysis
----------------------------------------------------
General metrics
IV 4.80825509
WoE 171.94601939
WoE (normalized) 7.63091898
HHI 0.08094955
HHI (normalized) 0.03917453
Quality score 0.00000067
Significance tests
Bin A Bin B t-statistic p-value
0 1 -0.626279 5.330261e-01
0 5 3.151772 2.418667e-03
1 2 -1.747295 1.020375e-01
1 6 7.166955 9.494930e-09
2 3 1.973052 7.794888e-02
2 7 5.476169 1.595659e-04
3 4 -0.603998 6.445191e-01
3 8 29.698485 2.142801e-02
4 12 7.038328 3.332810e-02
5 6 3.366820 1.818855e-03
5 9 -3.226180 1.104060e-02
6 7 0.226611 8.321374e-01
6 10 -3.751024 5.101241e-03
7 8 4.354171 1.437169e-01
7 11 -3.907609 2.230164e-03
8 4 -8.173675 7.750145e-02
8 11 -6.214215 1.015749e-01
9 10 0.399772 6.953661e-01
9 13 4.145039 4.969267e-03
10 11 -0.236693 8.157359e-01
10 14 3.489521 7.419876e-03
11 12 5.603629 1.405522e-04
11 15 4.844244 7.355489e-04
11 16 5.220987 2.298907e-04
12 20 0.507489 6.204418e-01
13 14 2.102164 3.968648e-02
13 17 2.752663 1.203338e-02
14 15 3.808928 2.644745e-04
14 17 1.559713 1.337095e-01
15 16 1.520196 1.429031e-01
15 18 0.901478 3.705578e-01
16 12 0.829910 4.281352e-01
16 19 -0.295271 7.688809e-01
17 18 1.239974 2.208911e-01
18 19 0.079654 9.366502e-01
19 20 1.517969 1.316990e-01
Mean monotonicity¶
The monotonic_trend_x and monotonic_trend_y options permit forcing a monotonic trend to the mean curve on each axis. By default, both options are set to None. There are two options available: “ascending” and “descending”. In this example, we force both trends to be “descending”, and a minimum bin size of 0.025 (2.5%).
[15]:
optb = ContinuousOptimalBinning2D(name_x=variable1, name_y=variable2,
monotonic_trend_x="descending",
monotonic_trend_y="descending", min_bin_size=0.025)
optb.fit(x, y, z)
[15]:
ContinuousOptimalBinning2D(min_bin_size=0.025, monotonic_trend_x='descending',
monotonic_trend_y='descending', name_x='AGE',
name_y='INDUS')
[16]:
optb.binning_table.build()
[16]:
| Bin x | Bin y | Count | Count (%) | Sum | Std | Mean | WoE | IV | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | (-inf, 92.30) | (-inf, 3.99) | 88 | 0.173913 | 2803.0 | 8.870303 | 31.852273 | 9.319466 | 1.620777 |
| 1 | [92.30, 98.25) | (-inf, 16.57) | 18 | 0.035573 | 344.2 | 5.806372 | 19.122222 | -3.410584 | 0.121325 |
| 2 | [98.25, inf) | (-inf, inf) | 58 | 0.114625 | 939.7 | 8.837625 | 16.201724 | -6.331082 | 0.725697 |
| 3 | (-inf, 37.25) | [3.99, 6.66) | 34 | 0.067194 | 913.1 | 6.300849 | 26.855882 | 4.323076 | 0.290483 |
| 4 | [37.25, 92.30) | [3.99, 6.66) | 59 | 0.116601 | 1471.2 | 7.247437 | 24.935593 | 2.402787 | 0.280167 |
| 5 | (-inf, 37.25) | [6.66, 16.57) | 23 | 0.045455 | 543.5 | 2.327610 | 23.630435 | 1.097628 | 0.049892 |
| 6 | [37.25, 76.25) | [6.66, 16.57) | 49 | 0.096838 | 1086.8 | 3.434815 | 22.179592 | -0.353214 | 0.034205 |
| 7 | [76.25, 92.30) | [6.66, 16.57) | 40 | 0.079051 | 777.0 | 3.359967 | 19.425000 | -3.107806 | 0.245676 |
| 8 | (-inf, 76.25) | [16.57, inf) | 16 | 0.031621 | 324.4 | 4.472765 | 20.275000 | -2.257806 | 0.071393 |
| 9 | [76.25, 92.30) | [16.57, inf) | 50 | 0.098814 | 912.5 | 8.416228 | 18.250000 | -4.282806 | 0.423202 |
| 10 | [92.30, 98.25) | [16.57, inf) | 71 | 0.140316 | 1286.2 | 10.093278 | 18.115493 | -4.417313 | 0.619821 |
| 11 | Special | Special | 0 | 0.000000 | 0.0 | 0.000000 | 0.000000 | -22.532806 | 0.000000 |
| 12 | Missing | Missing | 0 | 0.000000 | 0.0 | 0.000000 | 0.000000 | -22.532806 | 0.000000 |
| Totals | 506 | 1.000000 | 11401.6 | 22.532806 | 86.369184 | 4.482638 |
[17]:
optb.binning_table.plot()
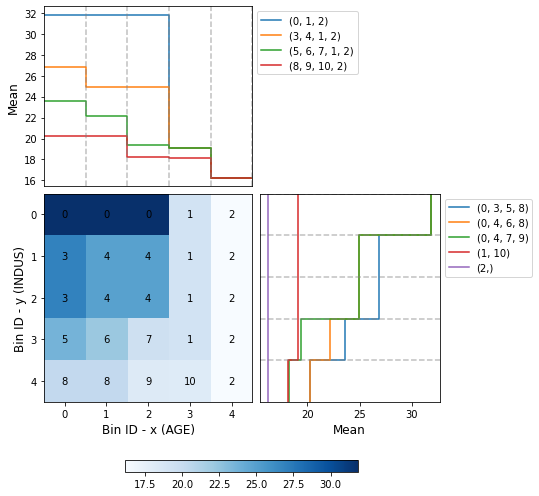
[18]:
optb.binning_table.analysis()
----------------------------------------------------
OptimalBinning: Continuous Binning Table 2D Analysis
----------------------------------------------------
General metrics
IV 4.48263838
WoE 86.36918355
WoE (normalized) 3.83304158
HHI 0.11090628
HHI (normalized) 0.03681514
Quality score 0.00064848
Significance tests
Bin A Bin B t-statistic p-value
0 1 7.652734 5.085335e-09
0 3 3.479643 7.978542e-04
0 4 5.177909 7.689996e-07
1 2 1.627628 1.108228e-01
1 10 0.553529 5.825586e-01
3 4 1.338602 1.846378e-01
3 5 2.722868 9.181932e-03
4 1 3.497175 1.308292e-03
4 6 2.591442 1.122681e-02
4 7 5.089123 2.035925e-06
5 6 2.102164 3.968648e-02
5 8 2.752663 1.203338e-02
6 7 3.808928 2.644745e-04
6 8 1.559713 1.337095e-01
7 1 0.206242 8.384742e-01
7 9 0.901478 3.705578e-01
8 9 1.239974 2.208911e-01
9 10 0.079654 9.366502e-01
10 2 1.147500 2.533428e-01
Mininum mean difference between consecutive bins¶
Now, we note that the mean difference between consecutive bins is not significant enough on the x-axis. Therefore, we decide to set min_mean_diff_x=2.0:
[19]:
optb = ContinuousOptimalBinning2D(name_x=variable1, name_y=variable2,
monotonic_trend_x="descending",
monotonic_trend_y="descending", min_bin_size=0.025,
min_mean_diff_x=2.0)
optb.fit(x, y, z)
[19]:
ContinuousOptimalBinning2D(min_bin_size=0.025, min_mean_diff_x=2.0,
monotonic_trend_x='descending',
monotonic_trend_y='descending', name_x='AGE',
name_y='INDUS')
[20]:
optb.binning_table.build()
[20]:
| Bin x | Bin y | Count | Count (%) | Sum | Std | Mean | WoE | IV | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | (-inf, inf) | (-inf, 3.99) | 92 | 0.181818 | 2932.6 | 8.688703 | 31.876087 | 9.343281 | 1.698778 |
| 1 | (-inf, 37.25) | [3.99, 6.66) | 34 | 0.067194 | 913.1 | 6.300849 | 26.855882 | 4.323076 | 0.290483 |
| 2 | [37.25, inf) | [3.99, 6.66) | 60 | 0.118577 | 1487.2 | 7.277258 | 24.786667 | 2.253860 | 0.267256 |
| 3 | (-inf, 76.25) | [6.66, 16.57) | 72 | 0.142292 | 1630.3 | 3.196475 | 22.643056 | 0.110249 | 0.015688 |
| 4 | [76.25, inf) | [6.66, 16.57) | 59 | 0.116601 | 1107.2 | 3.624755 | 18.766102 | -3.766705 | 0.439201 |
| 5 | (-inf, 76.25) | [16.57, inf) | 16 | 0.031621 | 324.4 | 4.472765 | 20.275000 | -2.257806 | 0.071393 |
| 6 | [76.25, 98.25) | [16.57, inf) | 121 | 0.239130 | 2198.7 | 9.436718 | 18.171074 | -4.361732 | 1.043023 |
| 7 | [98.25, inf) | [16.57, inf) | 52 | 0.102767 | 808.1 | 8.662280 | 15.540385 | -6.992422 | 0.718589 |
| 8 | Special | Special | 0 | 0.000000 | 0.0 | 0.000000 | 0.000000 | -22.532806 | 0.000000 |
| 9 | Missing | Missing | 0 | 0.000000 | 0.0 | 0.000000 | 0.000000 | -22.532806 | 0.000000 |
| Totals | 506 | 1.000000 | 11401.6 | 22.532806 | 78.474743 | 4.544411 |
[21]:
optb.binning_table.plot()
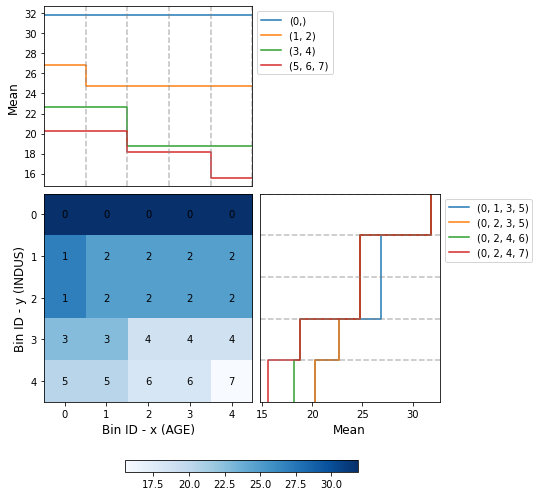
[22]:
optb.binning_table.analysis()
----------------------------------------------------
OptimalBinning: Continuous Binning Table 2D Analysis
----------------------------------------------------
General metrics
IV 4.54441094
WoE 78.47474349
WoE (normalized) 3.48268841
HHI 0.15422050
HHI (normalized) 0.06024500
Quality score 0.18196194
Significance tests
Bin A Bin B t-statistic p-value
0 1 3.560295 6.228004e-04
0 2 5.432189 2.380140e-07
1 2 1.445094 1.524836e-01
1 3 3.681359 6.667794e-04
2 3 2.117773 3.738699e-02
2 4 5.726516 1.440551e-07
3 4 6.420686 3.039622e-09
3 5 2.006927 5.955795e-02
4 6 0.607723 5.441768e-01
4 7 2.499373 1.491463e-02
5 6 1.492816 1.441306e-01
6 7 1.782159 7.762179e-02