Tutorial: Scorecard with continuous target

In this tutorial, we show that the use of scorecards is not limited to binary classification problems. We develop a scorecard using the Huber regressor as an estimator. The dataset for this tutorial is https://scikit-learn.org/stable/modules/generated/sklearn.datasets.fetch_california_housing.html.

import matplotlib.pyplot as plt
import pandas as pd

from sklearn.datasets import fetch_california_housing
from sklearn.linear_model import HuberRegressor

from optbinning import BinningProcess
from optbinning import Scorecard

Load the dataset.

data = fetch_california_housing()

target = "target"
variable_names = data.feature_names
X = pd.DataFrame(data.data, columns=variable_names)
y = data.target

X.head()

	MedInc	HouseAge	AveRooms	AveBedrms	Population	AveOccup	Latitude	Longitude
0	8.3252	41.0	6.984127	1.023810	322.0	2.555556	37.88	-122.23
1	8.3014	21.0	6.238137	0.971880	2401.0	2.109842	37.86	-122.22
2	7.2574	52.0	8.288136	1.073446	496.0	2.802260	37.85	-122.24
3	5.6431	52.0	5.817352	1.073059	558.0	2.547945	37.85	-122.25
4	3.8462	52.0	6.281853	1.081081	565.0	2.181467	37.85	-122.25

Then, we instantiate a BinningProcess object class with variable names.

binning_process = BinningProcess(variable_names)

We select a robust linear model as an estimator.

estimator = HuberRegressor(max_iter=200)

Finally, we instantiate a Scorecard class with the target name, a binning process object, and an estimator. In addition, we want to apply a scaling method to the scorecard points. Also, we select the reverse scorecard mode, so the score increases as the average house value increases.

scorecard = Scorecard(binning_process=binning_process,
                      estimator=estimator, scaling_method="min_max",
                      scaling_method_params={"min": 0, "max": 100},
                      reverse_scorecard=True)

scorecard.fit(X, y)

Scorecard(binning_process=BinningProcess(variable_names=['MedInc', 'HouseAge',
                                                         'AveRooms',
                                                         'AveBedrms',
                                                         'Population',
                                                         'AveOccup', 'Latitude',
                                                         'Longitude']),
          estimator=HuberRegressor(max_iter=200), reverse_scorecard=True,
          scaling_method='min_max',
          scaling_method_params={'max': 100, 'min': 0})

Similar to other objects in OptBinning, we can print overview information about the options settings, problems statistics, and the number of selected variables after the binning process.

scorecard.information(print_level=2)

optbinning (Version 0.19.0)
Copyright (c) 2019-2024 Guillermo Navas-Palencia, Apache License 2.0

  Begin options
    binning_process                      yes   * U
    estimator                            yes   * U
    scaling_method                   min_max   * U
    scaling_method_params                yes   * U
    intercept_based                    False   * d
    reverse_scorecard                   True   * U
    rounding                           False   * d
    verbose                            False   * d
  End options

  Statistics
    Number of records                  20640
    Number of variables                    8
    Target type                   continuous

    Number of numerical                    8
    Number of categorical                  0
    Number of selected                     8

  Timing
    Total time                          3.50 sec
    Binning process                     2.75 sec   ( 78.36%)
    Estimator                           0.61 sec   ( 17.36%)
    Build scorecard                     0.15 sec   (  4.23%)
      rounding                          0.00 sec   (  0.00%)

Two scorecard styles are available: style="summary" shows the variable name, and their corresponding bins and assigned points; style="detailed" adds information from the corresponding binning table.

scorecard.table(style="summary")

	Variable	Bin	Points
0	MedInc	(-inf, 1.90)	9.971931
1	MedInc	[1.90, 2.16)	11.050459
2	MedInc	[2.16, 2.37)	11.665492
3	MedInc	[2.37, 2.66)	12.845913
4	MedInc	[2.66, 2.88)	13.896692
...	...	...	...
3	Longitude	[-120.80, -119.76)	5.777181
4	Longitude	[-119.76, -118.91)	6.182494
5	Longitude	[-118.91, inf)	9.043458
6	Longitude	Special	1.059686
7	Longitude	Missing	1.059686

94 rows × 3 columns

scorecard.table(style="detailed")

	Variable	Bin id	Bin	Count	Count (%)	Sum	Std	Mean	Min	Max	Zeros count	WoE	IV	Coefficient	Points
0	MedInc	0	(-inf, 1.90)	2039	0.098789	2240.75810	0.711884	1.098950	0.14999	5.00001	0	-0.969609	0.095786	0.919860	9.971931
1	MedInc	1	[1.90, 2.16)	1109	0.053731	1366.22203	0.663722	1.231941	0.14999	5.00001	0	-0.836618	0.044952	0.919860	11.050459
2	MedInc	2	[2.16, 2.37)	1049	0.050824	1371.86004	0.706034	1.307779	0.17500	5.00001	0	-0.760779	0.038666	0.919860	11.665492
3	MedInc	3	[2.37, 2.66)	1551	0.075145	2254.12108	0.704002	1.453334	0.30000	5.00001	0	-0.615224	0.046231	0.919860	12.845913
4	MedInc	4	[2.66, 2.88)	1075	0.052083	1701.62105	0.756965	1.582903	0.22500	5.00001	0	-0.485655	0.025295	0.919860	13.896692
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
3	Longitude	3	[-120.80, -119.76)	1100	0.053295	1420.05208	0.793982	1.290956	0.28300	5.00001	0	-0.777602	0.041442	0.414488	5.777181
4	Longitude	4	[-119.76, -118.91)	1221	0.059157	1711.68530	1.074386	1.401872	0.26600	5.00001	0	-0.666687	0.039439	0.414488	6.182494
5	Longitude	5	[-118.91, inf)	10839	0.525145	23680.86379	1.119555	2.184783	0.14999	5.00001	0	0.116225	0.061035	0.414488	9.043458
6	Longitude	6	Special	0	0.000000	0.00000	NaN	0.000000	NaN	NaN	0	-2.068558	0.000000	0.414488	1.059686
7	Longitude	7	Missing	0	0.000000	0.00000	NaN	0.000000	NaN	NaN	0	-2.068558	0.000000	0.414488	1.059686

94 rows × 15 columns

Compute score and predicted target using the fitted estimator.

score = scorecard.score(X)

y_pred = scorecard.predict(X)

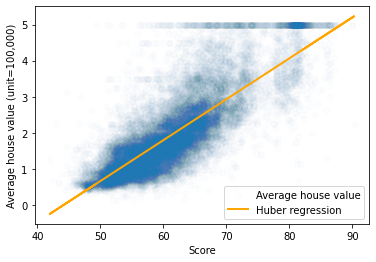
The following plot shows a perfect linear relationship between the score and average the house value.

plt.scatter(score, y, alpha=0.01, label="Average house value")
plt.plot(score, y_pred, label="Huber regression", linewidth=2, color="orange")
plt.ylabel("Average house value (unit=100,000)")
plt.xlabel("Score")
plt.legend()
plt.show()