Tutorial: optimal binning sketch with binary target¶
Stream processing¶
To get us started, let’s prepare the application_train.csv file from the Kaggle’s competition https://www.kaggle.com/c/home-credit-default-risk/data. This dataset will be used to simulate streaming data.
[1]:
import pandas as pd
[2]:
filepath = "data/kaggle/HomeCreditDefaultRisk/application_train.csv"
We choose a variable to discretize and the binary target.
[3]:
variable = "EXT_SOURCE_2"
target = "TARGET"
Import and instantiate an OptimalBinningSketch object class. We pass the variable name, its data type, and a solver, in this case, we choose the constraint programming solver. In addition, we pass the binning sketch type and the desired absolute precision.
[4]:
from optbinning import OptimalBinningSketch
[5]:
optbsketch = OptimalBinningSketch(name=variable, dtype="numerical", sketch="gk",
eps=1e-4, min_bin_size=0.05, solver="cp")
For simulating data streams, we read by chunks the dataset, adding arrays x and y of length 1000 to the optimal binning sketch object. If chunksize=1, we would add one single record at a time. Besides, we perform a solve every 10 additions to keep progress of the optimal binning sketch performance.
[6]:
chunks = pd.read_csv(filepath_or_buffer=filepath, engine='c', chunksize=1000,
usecols=[variable, target])
for k, chunk in enumerate(chunks):
x = chunk[variable].values
y = chunk[target].values
optbsketch.add(x, y)
if k % 10 == 0:
optbsketch.solve()
[7]:
optbsketch.solve()
[7]:
OptimalBinningSketch(min_bin_size=0.05, name='EXT_SOURCE_2')
You can check if an optimal solution has been found via the status attribute:
[8]:
optbsketch.status
[8]:
'OPTIMAL'
You can also retrieve the optimal split points via the splits attribute:
[9]:
optbsketch.splits
[9]:
array([0.21604822, 0.33976279, 0.39249913, 0.47915776, 0.56599903,
0.60839573, 0.64593877, 0.68204983, 0.72210817])
As in other binning classes in this library, method information is available to display overview information. This includes streaming statistics and timings such as the time spent in additions and solves, or the memory usage of the internal binning sketch. Note that the total time migth be significantly higher due to the time spent by pandas reading the CSV file. The remaining information is corresponding to the last solution.
[10]:
optbsketch.information(print_level=2)
optbinning (Version 0.19.0)
Copyright (c) 2019-2024 Guillermo Navas-Palencia, Apache License 2.0
Begin options
name EXT_SOURCE_2 * U
dtype numerical * d
sketch gk * d
eps 0.0001 * d
K 25 * d
solver cp * d
divergence iv * d
max_n_prebins 20 * d
min_n_bins no * d
max_n_bins no * d
min_bin_size 0.05 * U
max_bin_size no * d
min_bin_n_nonevent no * d
max_bin_n_nonevent no * d
min_bin_n_event no * d
max_bin_n_event no * d
monotonic_trend auto * d
min_event_rate_diff 0 * d
max_pvalue no * d
max_pvalue_policy consecutive * d
gamma 0 * d
cat_cutoff no * d
cat_unknown no * d
cat_heuristic False * d
special_codes no * d
split_digits no * d
mip_solver bop * d
time_limit 100 * d
verbose False * d
End options
Name : EXT_SOURCE_2
Status : OPTIMAL
Pre-binning statistics
Number of pre-bins 20
Number of refinements 0
Solver statistics
Type cp
Number of booleans 139
Number of branches 301
Number of conflicts 2
Objective value 307348
Best objective bound 307348
Timing
Total time 0.63 sec
Pre-binning 0.24 sec ( 37.76%)
Solver 0.39 sec ( 62.11%)
model generation 0.33 sec ( 85.40%)
optimizer 0.06 sec ( 14.60%)
Post-processing 0.00 sec ( 0.02%)
Streaming statistics
Sketch memory usage 4.25709 MB
Processed records 307511
Add operations 308
Solve operations 32
Streaming timing
Time add 1.44 sec (0.0047 sec / add)
Time solve 18.43 sec (0.5759 sec / solve)
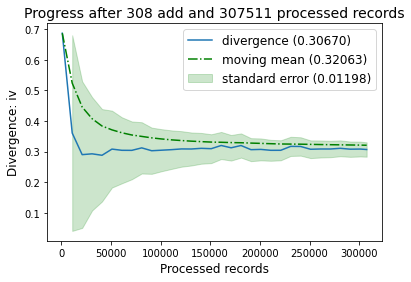
Since we have performed several solves throughout the process, we can observe the performance progress using method plot_progress. Observe the convergence and reduction of the standard error as new data is added.
[11]:
optbsketch.plot_progress()
The binning table¶
The optimal binning algorithms return a binning table; a binning table displays the binned data and several metrics for each bin. Class OptimalBinningSketch returns an object BinningTable via the binning_table attribute.
[12]:
optbsketch.binning_table.build()
[12]:
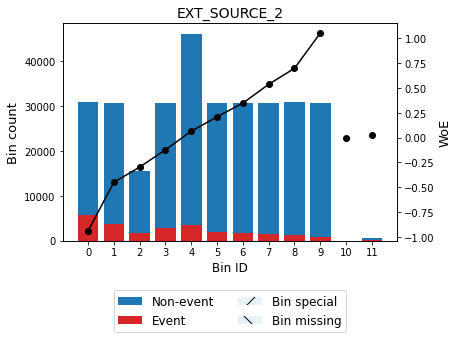
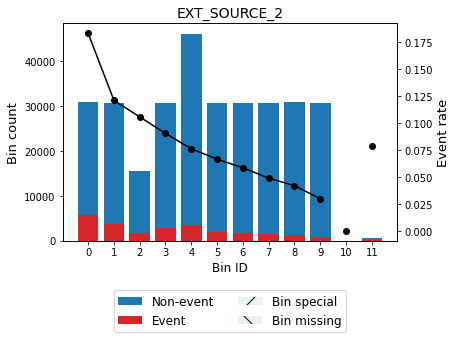
| Bin | Count | Count (%) | Non-event | Event | Event rate | WoE | IV | JS | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | (-inf, 0.22) | 30728 | 0.099925 | 25095 | 5633 | 0.183318 | -0.938459 | 0.129634 | 1.563463e-02 |
| 1 | [0.22, 0.34) | 30609 | 0.099538 | 26905 | 3704 | 0.121010 | -0.449587 | 0.024290 | 3.010977e-03 |
| 2 | [0.34, 0.39) | 15387 | 0.050037 | 13761 | 1626 | 0.105674 | -0.296770 | 0.004991 | 6.216437e-04 |
| 3 | [0.39, 0.48) | 30719 | 0.099896 | 27945 | 2774 | 0.090302 | -0.122538 | 0.001579 | 1.972682e-04 |
| 4 | [0.48, 0.57) | 46028 | 0.149679 | 42524 | 3504 | 0.076128 | 0.063678 | 0.000591 | 7.385673e-05 |
| 5 | [0.57, 0.61) | 30682 | 0.099775 | 28642 | 2040 | 0.066488 | 0.209439 | 0.004010 | 5.003169e-04 |
| 6 | [0.61, 0.65) | 30692 | 0.099808 | 28898 | 1794 | 0.058452 | 0.346839 | 0.010392 | 1.292468e-03 |
| 7 | [0.65, 0.68) | 30612 | 0.099548 | 29116 | 1496 | 0.048870 | 0.536007 | 0.022907 | 2.829549e-03 |
| 8 | [0.68, 0.72) | 30747 | 0.099987 | 29458 | 1289 | 0.041923 | 0.696613 | 0.036422 | 4.462842e-03 |
| 9 | [0.72, inf) | 30647 | 0.099661 | 29734 | 913 | 0.029791 | 1.050825 | 0.071883 | 8.593536e-03 |
| 10 | Special | 0 | 0.000000 | 0 | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000e+00 |
| 11 | Missing | 660 | 0.002146 | 608 | 52 | 0.078788 | 0.026446 | 0.000001 | 1.855558e-07 |
| Totals | 307511 | 1.000000 | 282686 | 24825 | 0.080729 | 0.306700 | 3.721727e-02 |
You can use the method plot to visualize the histogram and WoE or event rate curve. Note that the Bin ID corresponds to the binning table index.
[13]:
optbsketch.binning_table.plot(metric="woe")
[14]:
optbsketch.binning_table.plot(metric="event_rate")
Event rate / WoE transformation¶
Now that we have checked the binned data, we can transform our original data into WoE or event rate values. You can check the correctness of the transformation using pandas value_counts method, for instance. The transform method is handy to transform streaming data with the current binning sketch or after the fitting of the binning sketch has been completed.
[15]:
x = [0.2, 0.31, 0.21, 0.12, 0.16, 0.41, 0.65, 0.8]
[16]:
x_transform_woe = optbsketch.transform(x, metric="woe")
[17]:
pd.Series(x_transform_woe).value_counts()
[17]:
-0.938459 4
-0.449587 1
1.050825 1
0.536007 1
-0.122538 1
dtype: int64
[18]:
x_transform_event_rate = optbsketch.transform(x, metric="event_rate")
[19]:
pd.Series(x_transform_event_rate).value_counts()
[19]:
0.183318 4
0.090302 1
0.048870 1
0.121010 1
0.029791 1
dtype: int64
[20]:
x_transform_indices = optbsketch.transform(x, metric="indices")
[21]:
pd.Series(x_transform_indices).value_counts()
[21]:
0 4
1 1
3 1
9 1
7 1
dtype: int64
[22]:
x_transform_bins = optbsketch.transform(x, metric="bins")
[23]:
pd.Series(x_transform_bins).value_counts()
[23]:
(-inf, 0.22) 4
[0.39, 0.48) 1
[0.72, inf) 1
[0.22, 0.34) 1
[0.65, 0.68) 1
dtype: int64
Categorical variable¶
[24]:
variable_cat = "NAME_INCOME_TYPE"
We instantiate an OptimalBinningSketch object class with the variable name, its data type (categorical) and a solver, in this case, we choose the mixed-integer programming solver. Also, for this particular example, we set a cat_cutoff=0.1 to create bin others with categories in which the percentage of occurrences is below 10%. This will merge categories State servant, Unemployed, Student, Businessman and Maternity leave.
[25]:
optbsketch = OptimalBinningSketch(name=variable_cat, dtype="categorical", solver="mip",
min_bin_size=0.05, cat_cutoff=0.1)
Similar to the previous case, we simulate streaming data and perform several solves throughout the process.
[26]:
chunks = pd.read_csv(filepath_or_buffer=filepath, engine='c', chunksize=100,
usecols=[variable_cat, target])
for k, chunk in enumerate(chunks):
x = chunk[variable_cat].values
y = chunk[target].values
optbsketch.add(x, y)
if k % 100 == 0:
optbsketch.solve()
[27]:
optbsketch.solve()
[27]:
OptimalBinningSketch(cat_cutoff=0.1, dtype='categorical', min_bin_size=0.05,
name='NAME_INCOME_TYPE', solver='mip')
[28]:
optbsketch.status
[28]:
'OPTIMAL'
The optimal split points are the list of classes belonging to each bin.
[29]:
optbsketch.splits
[29]:
[array(['Pensioner'], dtype=object),
array(['Commercial associate'], dtype=object),
array(['Working'], dtype=object),
array(['State servant', 'Unemployed', 'Student', 'Businessman',
'Maternity leave'], dtype=object)]
Note that for categorical data, the time per add and memory usage is significantly reduced.
[30]:
optbsketch.information(print_level=2)
optbinning (Version 0.19.0)
Copyright (c) 2019-2024 Guillermo Navas-Palencia, Apache License 2.0
Begin options
name NAME_INCOME_TYPE * U
dtype categorical * U
sketch gk * d
eps 0.0001 * d
K 25 * d
solver mip * U
divergence iv * d
max_n_prebins 20 * d
min_n_bins no * d
max_n_bins no * d
min_bin_size 0.05 * U
max_bin_size no * d
min_bin_n_nonevent no * d
max_bin_n_nonevent no * d
min_bin_n_event no * d
max_bin_n_event no * d
monotonic_trend auto * d
min_event_rate_diff 0 * d
max_pvalue no * d
max_pvalue_policy consecutive * d
gamma 0 * d
cat_cutoff 0.1 * U
cat_unknown no * d
cat_heuristic False * d
special_codes no * d
split_digits no * d
mip_solver bop * d
time_limit 100 * d
verbose False * d
End options
Name : NAME_INCOME_TYPE
Status : OPTIMAL
Pre-binning statistics
Number of pre-bins 3
Number of refinements 0
Solver statistics
Type mip
Number of variables 12
Number of constraints 6
Objective value 0.0524
Best objective bound 0.0524
Timing
Total time 0.00 sec
Pre-binning 0.00 sec ( 16.42%)
Solver 0.00 sec ( 80.55%)
Post-processing 0.00 sec ( 2.56%)
Streaming statistics
Sketch memory usage 0.00280 MB
Processed records 307511
Add operations 3076
Solve operations 32
Streaming timing
Time add 0.91 sec (0.0003 sec / add)
Time solve 0.15 sec (0.0047 sec / solve)
[31]:
optbsketch.plot_progress()
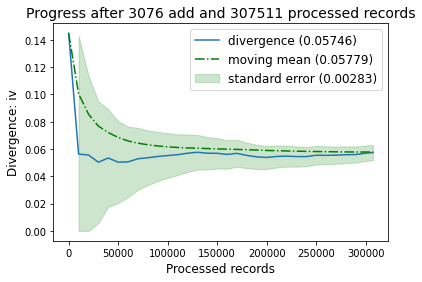
[32]:
optbsketch.binning_table.build()
[32]:
| Bin | Count | Count (%) | Non-event | Event | Event rate | WoE | IV | JS | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | [Pensioner] | 55362 | 0.180033 | 52380 | 2982 | 0.053864 | 0.433445 | 0.028249 | 0.003504 |
| 1 | [Commercial associate] | 71617 | 0.232892 | 66257 | 5360 | 0.074843 | 0.082092 | 0.001516 | 0.000189 |
| 2 | [Working] | 158774 | 0.516320 | 143550 | 15224 | 0.095885 | -0.188675 | 0.019895 | 0.002483 |
| 3 | [State servant, Unemployed, Student, Businessm... | 21758 | 0.070755 | 20499 | 1259 | 0.057864 | 0.357573 | 0.007795 | 0.000969 |
| 4 | Special | 0 | 0.000000 | 0 | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 5 | Missing | 0 | 0.000000 | 0 | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| Totals | 307511 | 1.000000 | 282686 | 24825 | 0.080729 | 0.057455 | 0.007146 |
You can use the method plot to visualize the histogram and WoE or event rate curve. Note that for categorical variables the optimal bins are always monotonically ascending with respect to the event rate. Finally, note that bin 3 corresponds to bin others and is represented by using a lighter color.
[33]:
optbsketch.binning_table.plot(metric="event_rate")
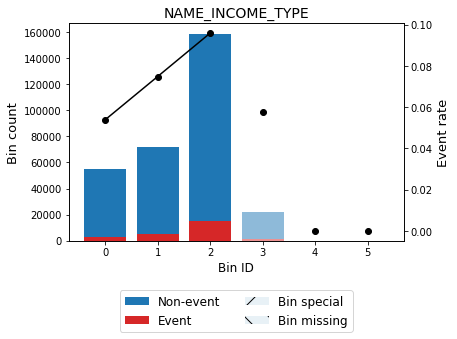
Same as for the numerical dtype, we can transform our original data into WoE or event rate values. Transformation of data including categories not present during training return zero WoE or event rate.
[34]:
x_new = ["Businessman", "Working", "Unknown"]
[35]:
x_transform_woe = optbsketch.transform(x_new, metric="woe")
[36]:
pd.DataFrame({variable_cat: x_new, "WoE": x_transform_woe})
[36]:
| NAME_INCOME_TYPE | WoE | |
|---|---|---|
| 0 | Businessman | 0.357573 |
| 1 | Working | -0.188675 |
| 2 | Unknown | 0.000000 |
Batch processing¶
The new OptimalBinningSketch class permits several new use cases:
Case 1: Optimal binning using datasets with the same structure stored on a distributed infrastructure. No data centralization.
Case 2: Optimal binning for very large datasets that do not fit in memory.
Case 3: Optimal binning suitable for federated learning. The training data is kept on the device, only the OptimalBinningSketch class is sent to the cloud, where it is merged.
In this example, we have three partitions of a dataset. For faster columnar access we use parquet
[37]:
filepaths = ["data/df1.parquet.gzip",
"data/df2.parquet.gzip",
"data/df3.parquet.gzip"]
[38]:
variable = "EXT_SOURCE_3"
target = "TARGET"
We create a simple map-reduce structure
[39]:
from functools import reduce
[40]:
def add(filepath):
df = pd.read_parquet(path=filepath, columns=[variable, target])
x = df[variable].values
y = df[target].values
optbsketch = OptimalBinningSketch(name=variable, dtype="numerical",
sketch="gk", min_bin_size=0.05)
optbsketch.add(x, y)
return optbsketch
def merge(optbsketch, other_optbsketch):
optbsketch.merge(other_optbsketch)
return optbsketch
optbsketch = reduce(merge, map(add, filepaths))
[41]:
optbsketch.solve()
[41]:
OptimalBinningSketch(min_bin_size=0.05, name='EXT_SOURCE_3')
[42]:
optbsketch.information()
optbinning (Version 0.19.0)
Copyright (c) 2019-2024 Guillermo Navas-Palencia, Apache License 2.0
Name : EXT_SOURCE_3
Status : OPTIMAL
Pre-binning statistics
Number of pre-bins 20
Number of refinements 0
Solver statistics
Type cp
Number of booleans 117
Number of branches 255
Number of conflicts 2
Objective value 411345
Best objective bound 411345
Timing
Total time 0.79 sec
Pre-binning 0.44 sec ( 56.07%)
Solver 0.35 sec ( 43.81%)
model generation 0.29 sec ( 84.69%)
optimizer 0.05 sec ( 15.31%)
Post-processing 0.00 sec ( 0.02%)
Streaming statistics
Sketch memory usage 9.31202 MB
Processed records 307511
Add operations 1
Solve operations 1
Streaming timing
Time add 0.52 sec (0.5156 sec / add)
Time solve 0.79 sec (0.7906 sec / solve)
[43]:
optbsketch.binning_table.build()
[43]:
| Bin | Count | Count (%) | Non-event | Event | Event rate | WoE | IV | JS | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | (-inf, 0.23) | 24912 | 0.081012 | 19934 | 4978 | 0.199823 | -1.045087 | 0.135869 | 0.016251 |
| 1 | [0.23, 0.33) | 24475 | 0.079591 | 21357 | 3118 | 0.127395 | -0.508298 | 0.025440 | 0.003146 |
| 2 | [0.33, 0.41) | 25058 | 0.081487 | 22675 | 2383 | 0.095099 | -0.179583 | 0.002834 | 0.000354 |
| 3 | [0.41, 0.48) | 24687 | 0.080280 | 22718 | 1969 | 0.079759 | 0.013146 | 0.000014 | 0.000002 |
| 4 | [0.48, 0.56) | 36860 | 0.119866 | 34644 | 2216 | 0.060119 | 0.316935 | 0.010550 | 0.001313 |
| 5 | [0.56, 0.62) | 24858 | 0.080836 | 23606 | 1252 | 0.050366 | 0.504273 | 0.016678 | 0.002063 |
| 6 | [0.62, 0.67) | 24647 | 0.080150 | 23565 | 1082 | 0.043900 | 0.648466 | 0.025793 | 0.003169 |
| 7 | [0.67, 0.72) | 24067 | 0.078264 | 23128 | 939 | 0.039016 | 0.771498 | 0.033939 | 0.004140 |
| 8 | [0.72, inf) | 36982 | 0.120262 | 35771 | 1211 | 0.032746 | 0.953206 | 0.074120 | 0.008929 |
| 9 | Special | 0 | 0.000000 | 0 | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 10 | Missing | 60965 | 0.198253 | 55288 | 5677 | 0.093119 | -0.156353 | 0.005175 | 0.000646 |
| Totals | 307511 | 1.000000 | 282686 | 24825 | 0.080729 | 0.330411 | 0.040013 |
[44]:
optbsketch.binning_table.plot(metric="event_rate")
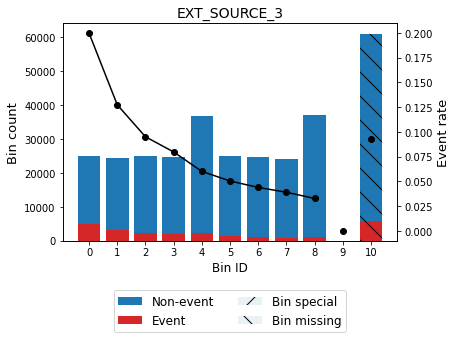
[45]:
optbsketch.binning_table.analysis()
---------------------------------------------
OptimalBinning: Binary Binning Table Analysis
---------------------------------------------
General metrics
Gini index 0.31382475
IV (Jeffrey) 0.33041081
JS (Jensen-Shannon) 0.04001304
Hellinger 0.04064260
Triangular 0.15533757
KS 0.19583547
HHI 0.11320133
HHI (normalized) 0.02452146
Cramer's V 0.18562733
Quality score 0.94042182
Monotonic trend descending
Significance tests
Bin A Bin B t-statistic p-value P[A > B] P[B > A]
0 1 472.532789 9.007791e-105 1.000000 1.110223e-16
1 2 130.812523 2.721311e-30 1.000000 1.110223e-16
2 3 36.659113 1.406997e-09 1.000000 7.681411e-12
3 4 89.982629 2.402603e-21 1.000000 1.110223e-16
4 5 26.629360 2.464697e-07 1.000000 1.861165e-09
5 6 11.518699 6.889960e-04 0.999754 2.460969e-04
6 7 7.303566 6.881789e-03 0.996897 3.102626e-03
7 8 16.870882 4.001068e-05 0.999986 1.404877e-05