Tutorial: optimal piecewise binning with continuous target¶
Basic¶
To get us started, let’s load a well-known dataset from the UCI repository and transform the data into a pandas.DataFrame.
[1]:
import pandas as pd
from tests.datasets import load_boston
[2]:
data = load_boston()
df = pd.DataFrame(data.data, columns=data.feature_names)
We choose a variable to discretize and the continuous target.
[3]:
variable = "LSTAT"
x = df[variable].values
y = data.target
Import and instantiate an ContinuousOptimalPWBinning object class and we pass the variable name. The ContinuousOptimalPWBinning can ONLY handle numerical variables. This differs from the ContinuousOptimalBinning object class.
[4]:
from optbinning import ContinuousOptimalPWBinning
[5]:
optb = ContinuousOptimalPWBinning(name=variable)
We fit the optimal binning object with arrays x and y.
[6]:
optb.fit(x, y)
[6]:
ContinuousOptimalPWBinning(name='LSTAT')
You can check if an optimal solution has been found via the status attribute:
[7]:
optb.status
[7]:
'OPTIMAL'
You can also retrieve the optimal split points via the splits attribute:
[8]:
optb.splits
[8]:
array([ 4.6500001 , 5.49499989, 6.86500001, 9.7249999 , 13.0999999 ,
14.4000001 , 17.23999977, 19.89999962, 23.31500053])
The binning table¶
The optimal binning algorithms return a binning table; a binning table displays the binned data and several metrics for each bin. Class ContinuousOptimalPWBinning returns an object PWContinuousBinningTable via the binning_table attribute.
[9]:
binning_table = optb.binning_table
[10]:
type(binning_table)
[10]:
optbinning.binning.piecewise.binning_statistics.PWContinuousBinningTable
The binning_table is instantiated, but not built. Therefore, the first step is to call the method build, which returns a pandas.DataFrame.
[11]:
binning_table.build()
[11]:
| Bin | Count | Count (%) | Sum | Std | Min | Max | Zeros count | c0 | c1 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | (-inf, 4.65) | 50.0 | 0.098814 | 1985.9 | 8.198651 | 22.8 | 50.0 | 0 | 56.744157 | -4.821782 |
| 1 | [4.65, 5.49) | 28.0 | 0.055336 | 853.2 | 6.123541 | 21.9 | 50.0 | 0 | 74.661294 | -8.674929 |
| 2 | [5.49, 6.87) | 45.0 | 0.088933 | 1188.6 | 5.136259 | 20.6 | 48.8 | 0 | 26.992559 | -0.000000 |
| 3 | [6.87, 9.72) | 89.0 | 0.175889 | 2274.9 | 6.845250 | 11.9 | 50.0 | 0 | 36.396429 | -1.369828 |
| 4 | [9.72, 13.10) | 84.0 | 0.166008 | 1755.4 | 2.949979 | 14.5 | 31.0 | 0 | 31.699081 | -0.886810 |
| 5 | [13.10, 14.40) | 32.0 | 0.063241 | 667.4 | 2.632482 | 15.0 | 29.6 | 0 | 27.030856 | -0.530457 |
| 6 | [14.40, 17.24) | 60.0 | 0.118577 | 1037.5 | 3.588003 | 10.2 | 30.7 | 0 | 35.230331 | -1.099865 |
| 7 | [17.24, 19.90) | 43.0 | 0.084980 | 714.3 | 4.032554 | 8.3 | 27.5 | 0 | 23.261993 | -0.405646 |
| 8 | [19.90, 23.32) | 28.0 | 0.055336 | 368.4 | 3.912839 | 5.0 | 21.7 | 0 | 33.251552 | -0.907634 |
| 9 | [23.32, inf) | 47.0 | 0.092885 | 556.0 | 4.006586 | 5.0 | 23.7 | 0 | 13.222398 | -0.048567 |
| 10 | Special | 0.0 | 0.000000 | 0.0 | None | None | None | 0 | 0.000000 | 0.000000 |
| 11 | Missing | 0.0 | 0.000000 | 0.0 | None | None | None | 0 | 0.000000 | 0.000000 |
| Totals | 506.0 | 1.000000 | 11401.6 | 5.0 | 50.0 | 0 | - | - |
Let’s describe the columns of this binning table:
Bin: the intervals delimited by the optimal split points.
Count: the number of records for each bin.
Count (%): the percentage of records for each bin.
Sum: the target sum for each bin.
Std: the target std for each bin.
Min: the target min value for each bin.
Max: the target max value for each bin.
Zeros count: the number of zeros for each bin.
\(c_0\): the first coefficient of the prediction polynomial.
\(c_1\): the second coefficient of the prediction polynomial.
The for bin \(i\) is defined as \(P_i = c_0 + c_1 x_i\), where \(x_i \in \text{Bin}_{i}\). In general, \begin{equation} P_i = \sum_{j=0}^d c_j x_i^j, \end{equation} where \(d\) is the degree of the event rate polynomial.
The last row shows the total number of records, sum and mean.
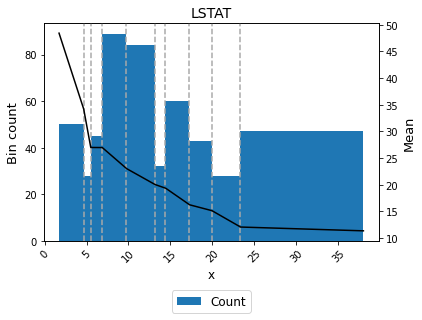
You can use the method plot to visualize the histogram and mean curve.
[12]:
binning_table.plot()
Mean transformation¶
Now that we have checked the binned data, we can transform our original data into mean values.
[13]:
x_transform_mean = optb.transform(x)
Advanced¶
Many of the advanced options have been covered in the previous tutorials with a binary target. Check it out! In this section, we focus on the mean monotonicity trend and the mean difference between bins.
Binning table statistical analysis¶
The analysis method performs a statistical analysis of the binning table, computing the Information Value (IV) and Herfindahl-Hirschman Index (HHI). Additionally, several statistical significance tests between consecutive bins of the contingency table are performed using the Student’s t-test. The piecewise binning also includes several performance metrics for regression problems.
[14]:
binning_table.analysis()
-------------------------------------------------
OptimalBinning: Continuous Binning Table Analysis
-------------------------------------------------
General metrics
Mean absolute error 3.67892091
Mean squared error 26.06425104
Median absolute error 2.71794576
Explained variance 0.69125340
R^2 0.69125340
MPE -0.05221127
MAPE 0.17785599
SMAPE 0.08395478
MdAPE 0.13052555
SMdAPE 0.06542912
HHI 0.11620241
HHI (normalized) 0.03585717
Quality score 0.01671264
Significance tests
Bin A Bin B t-statistic p-value
0 1 5.644492 3.313748e-07
1 2 2.924528 5.175586e-03
2 3 0.808313 4.206096e-01
3 4 5.874488 3.816654e-08
4 5 0.073112 9.419504e-01
5 6 5.428848 5.770714e-07
6 7 0.883289 3.796030e-01
7 8 3.591859 6.692488e-04
8 9 1.408305 1.643801e-01
[15]:
binning_table.analysis()
-------------------------------------------------
OptimalBinning: Continuous Binning Table Analysis
-------------------------------------------------
General metrics
Mean absolute error 3.67892091
Mean squared error 26.06425104
Median absolute error 2.71794576
Explained variance 0.69125340
R^2 0.69125340
MPE -0.05221127
MAPE 0.17785599
SMAPE 0.08395478
MdAPE 0.13052555
SMdAPE 0.06542912
HHI 0.11620241
HHI (normalized) 0.03585717
Quality score 0.01671264
Significance tests
Bin A Bin B t-statistic p-value
0 1 5.644492 3.313748e-07
1 2 2.924528 5.175586e-03
2 3 0.808313 4.206096e-01
3 4 5.874488 3.816654e-08
4 5 0.073112 9.419504e-01
5 6 5.428848 5.770714e-07
6 7 0.883289 3.796030e-01
7 8 3.591859 6.692488e-04
8 9 1.408305 1.643801e-01
Mean monotonicity¶
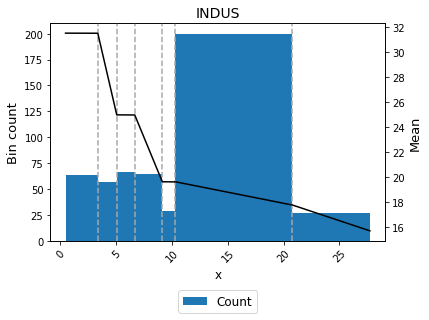
The monotonic_trend option permits forcing a monotonic trend to the mean curve. The default setting “auto” should be the preferred option, however, some business constraints might require to impose different trends. The default setting “auto” chooses the monotonic trend most likely to minimize the L1-norm from the options “ascending”, “descending”, “peak” and “valley” using a machine-learning-based classifier.
[16]:
variable = "INDUS"
x = df[variable].values
y = data.target
[17]:
optb = ContinuousOptimalPWBinning(name=variable, monotonic_trend="auto")
optb.fit(x, y)
[17]:
ContinuousOptimalPWBinning(name='INDUS')
[18]:
binning_table = optb.binning_table
binning_table.build()
[18]:
| Bin | Count | Count (%) | Sum | Std | Min | Max | Zeros count | c0 | c1 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | (-inf, 3.35) | 63.0 | 0.124506 | 1994.0 | 8.569841 | 16.5 | 50.0 | 0 | 31.494243 | 0.000000 |
| 1 | [3.35, 5.04) | 57.0 | 0.112648 | 1615.2 | 8.072710 | 17.2 | 50.0 | 0 | 44.441955 | -3.864989 |
| 2 | [5.04, 6.66) | 66.0 | 0.130435 | 1723.7 | 7.879078 | 16.0 | 50.0 | 0 | 24.962412 | 0.000000 |
| 3 | [6.66, 9.12) | 64.0 | 0.126482 | 1292.0 | 4.614126 | 12.7 | 35.2 | 0 | 39.414039 | -2.169914 |
| 4 | [9.12, 10.30) | 29.0 | 0.057312 | 584.1 | 2.252281 | 16.1 | 24.5 | 0 | 19.613573 | 0.000000 |
| 5 | [10.30, 20.73) | 200.0 | 0.395257 | 3736.2 | 8.959305 | 5.0 | 50.0 | 0 | 21.429532 | -0.176307 |
| 6 | [20.73, inf) | 27.0 | 0.053360 | 456.4 | 3.690878 | 7.0 | 23.0 | 0 | 23.933551 | -0.297070 |
| 7 | Special | 0.0 | 0.000000 | 0.0 | None | None | None | 0 | 0.000000 | 0.000000 |
| 8 | Missing | 0.0 | 0.000000 | 0.0 | None | None | None | 0 | 0.000000 | 0.000000 |
| Totals | 506.0 | 1.000000 | 11401.6 | 5.0 | 50.0 | 0 | - | - |
[19]:
binning_table.plot()
[20]:
binning_table.analysis()
-------------------------------------------------
OptimalBinning: Continuous Binning Table Analysis
-------------------------------------------------
General metrics
Mean absolute error 5.44142744
Mean squared error 59.78870565
Median absolute error 4.13838129
Explained variance 0.29176712
R^2 0.29176712
MPE -0.12274348
MAPE 0.28239036
SMAPE 0.12302499
MdAPE 0.19474014
SMdAPE 0.09639011
HHI 0.22356231
HHI (normalized) 0.12650760
Quality score 0.03355055
Significance tests
Bin A Bin B t-statistic p-value
0 1 2.180865 3.118080e-02
1 2 1.537968 1.267445e-01
2 3 5.254539 7.781110e-07
3 4 0.064736 9.485275e-01
4 5 1.923770 5.601023e-02
5 6 1.867339 6.563949e-02
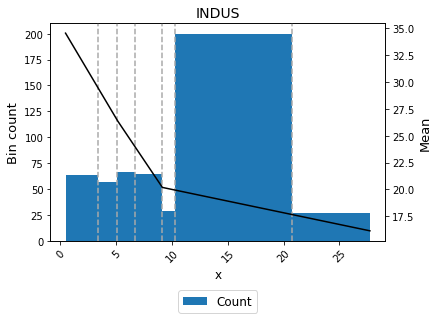
A smoother curve, keeping the valley monotonicity, can be achieved by using monotonic_trend="convex".
[21]:
optb = ContinuousOptimalPWBinning(name=variable, monotonic_trend="convex")
optb.fit(x, y)
[21]:
ContinuousOptimalPWBinning(monotonic_trend='convex', name='INDUS')
[22]:
binning_table = optb.binning_table
binning_table.build()
[22]:
| Bin | Count | Count (%) | Sum | Std | Min | Max | Zeros count | c0 | c1 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | (-inf, 3.35) | 63.0 | 0.124506 | 1994.0 | 8.569841 | 16.5 | 50.0 | 0 | 35.353511 | -1.753581 |
| 1 | [3.35, 5.04) | 57.0 | 0.112648 | 1615.2 | 8.072710 | 17.2 | 50.0 | 0 | 35.353511 | -1.753581 |
| 2 | [5.04, 6.66) | 66.0 | 0.130435 | 1723.7 | 7.879078 | 16.0 | 50.0 | 0 | 34.324955 | -1.549503 |
| 3 | [6.66, 9.12) | 64.0 | 0.126482 | 1292.0 | 4.614126 | 12.7 | 35.2 | 0 | 34.324955 | -1.549503 |
| 4 | [9.12, 10.30) | 29.0 | 0.057312 | 584.1 | 2.252281 | 16.1 | 24.5 | 0 | 22.168554 | -0.217294 |
| 5 | [10.30, 20.73) | 200.0 | 0.395257 | 3736.2 | 8.959305 | 5.0 | 50.0 | 0 | 22.168554 | -0.217294 |
| 6 | [20.73, inf) | 27.0 | 0.053360 | 456.4 | 3.690878 | 7.0 | 23.0 | 0 | 22.168554 | -0.217294 |
| 7 | Special | 0.0 | 0.000000 | 0.0 | None | None | None | 0 | 0.000000 | 0.000000 |
| 8 | Missing | 0.0 | 0.000000 | 0.0 | None | None | None | 0 | 0.000000 | 0.000000 |
| Totals | 506.0 | 1.000000 | 11401.6 | 5.0 | 50.0 | 0 | - | - |
[23]:
binning_table.plot()
[24]:
binning_table.analysis()
-------------------------------------------------
OptimalBinning: Continuous Binning Table Analysis
-------------------------------------------------
General metrics
Mean absolute error 5.51198416
Mean squared error 60.76046517
Median absolute error 4.19400512
Explained variance 0.28025605
R^2 0.28025605
MPE -0.12411637
MAPE 0.28485622
SMAPE 0.12424799
MdAPE 0.19529048
SMdAPE 0.09815566
HHI 0.22356231
HHI (normalized) 0.12650760
Quality score 0.03355055
Significance tests
Bin A Bin B t-statistic p-value
0 1 2.180865 3.118080e-02
1 2 1.537968 1.267445e-01
2 3 5.254539 7.781110e-07
3 4 0.064736 9.485275e-01
4 5 1.923770 5.601023e-02
5 6 1.867339 6.563949e-02