Tutorial: optimal binning with continuous target¶
Basic¶
To get us started, let’s load a well-known dataset from the UCI repository and transform the data into a pandas.DataFrame.
[1]:
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from tests.datasets import load_boston
[2]:
data = load_boston()
df = pd.DataFrame(data.data, columns=data.feature_names)
We choose a variable to discretize and the continuous target.
[3]:
variable = "LSTAT"
x = df[variable].values
y = data.target
Import and instantiate an ContinuousOptimalBinning object class. We pass the variable name and its data type.
[4]:
from optbinning import ContinuousOptimalBinning
[5]:
optb = ContinuousOptimalBinning(name=variable, dtype="numerical")
We fit the optimal binning object with arrays x and y.
[6]:
optb.fit(x, y)
[6]:
ContinuousOptimalBinning(name='LSTAT')
You can check if an optimal solution has been found via the status attribute:
[7]:
optb.status
[7]:
'OPTIMAL'
You can also retrieve the optimal split points via the splits attribute:
[8]:
optb.splits
[8]:
array([ 4.6500001 , 5.49499989, 6.86500001, 9.7249999 , 13.0999999 ,
14.4000001 , 17.23999977, 19.89999962, 23.31500053])
The binning table¶
The optimal binning algorithms return a binning table; a binning table displays the binned data and several metrics for each bin. Class ContinuousOptimalBinning returns an object ContinuousBinningTable via the binning_table attribute.
[9]:
binning_table = optb.binning_table
[10]:
type(binning_table)
[10]:
optbinning.binning.binning_statistics.ContinuousBinningTable
The binning_table is instantiated, but not built. Therefore, the first step is to call the method build, which returns a pandas.DataFrame.
[11]:
binning_table.build()
[11]:
| Bin | Count | Count (%) | Sum | Std | Mean | Min | Max | Zeros count | WoE | IV | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | (-inf, 4.65) | 50 | 0.098814 | 1985.9 | 8.198651 | 39.718000 | 22.8 | 50.0 | 0 | 17.185194 | 1.698142 |
| 1 | [4.65, 5.49) | 28 | 0.055336 | 853.2 | 6.123541 | 30.471429 | 21.9 | 50.0 | 0 | 7.938622 | 0.439291 |
| 2 | [5.49, 6.87) | 45 | 0.088933 | 1188.6 | 5.136259 | 26.413333 | 20.6 | 48.8 | 0 | 3.880527 | 0.345106 |
| 3 | [6.87, 9.72) | 89 | 0.175889 | 2274.9 | 6.845250 | 25.560674 | 11.9 | 50.0 | 0 | 3.027868 | 0.532570 |
| 4 | [9.72, 13.10) | 84 | 0.166008 | 1755.4 | 2.949979 | 20.897619 | 14.5 | 31.0 | 0 | -1.635187 | 0.271454 |
| 5 | [13.10, 14.40) | 32 | 0.063241 | 667.4 | 2.632482 | 20.856250 | 15.0 | 29.6 | 0 | -1.676556 | 0.106027 |
| 6 | [14.40, 17.24) | 60 | 0.118577 | 1037.5 | 3.588003 | 17.291667 | 10.2 | 30.7 | 0 | -5.241140 | 0.621479 |
| 7 | [17.24, 19.90) | 43 | 0.084980 | 714.3 | 4.032554 | 16.611628 | 8.3 | 27.5 | 0 | -5.921178 | 0.503183 |
| 8 | [19.90, 23.32) | 28 | 0.055336 | 368.4 | 3.912839 | 13.157143 | 5.0 | 21.7 | 0 | -9.375663 | 0.518811 |
| 9 | [23.32, inf) | 47 | 0.092885 | 556.0 | 4.006586 | 11.829787 | 5.0 | 23.7 | 0 | -10.703019 | 0.994154 |
| 10 | Special | 0 | 0.000000 | 0.0 | NaN | 0.000000 | NaN | NaN | 0 | -22.532806 | 0.000000 |
| 11 | Missing | 0 | 0.000000 | 0.0 | NaN | 0.000000 | NaN | NaN | 0 | -22.532806 | 0.000000 |
| Totals | 506 | 1.000000 | 11401.6 | 22.532806 | 5.0 | 50.0 | 0 | 111.650568 | 6.030218 |
Let’s describe the columns of this binning table:
Bin: the intervals delimited by the optimal split points.
Count: the number of records for each bin.
Count (%): the percentage of records for each bin.
Sum: the target sum for each bin.
Std: the target std for each bin.
Mean: the target mean for each bin.
Min: the target min value for each bin.
Max: the target max value for each bin.
Zeros count: the number of zeros for each bin.
WoE: Surrogate Weight-of-Evidence for each bin.
IV: Surrogate IV for each bin.
The WoE IV for a continuous target is computed as follows:
\begin{equation} IV = \sum_{i=1}^n \text{WoE}_i \frac{r_i}{r_T}, \quad \text{WoE}_i = |U_i - \mu|, \end{equation}
where \(U_i\) is the target mean value for each bin, \(\mu\) is the total target mean, \(r_i\) is the number of records for each bin, and \(r_T\) is the total number of records.
The last row shows the total number of records, sum and mean.
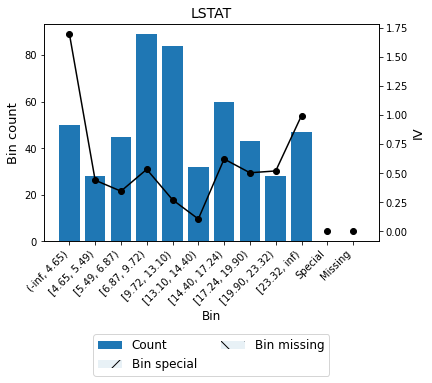
You can use the method plot to visualize the histogram and mean curve. Note that the Bin ID corresponds to the binning table index.
[12]:
binning_table.plot()
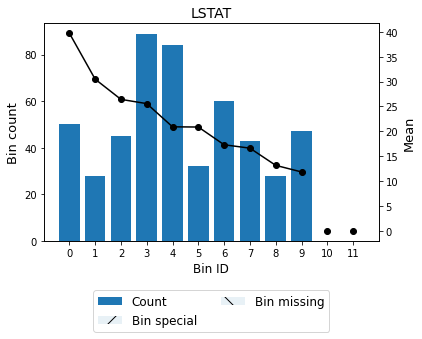
Optionally, you can show the binning plot with the actual bin widths.
[13]:
binning_table.plot(style="actual")
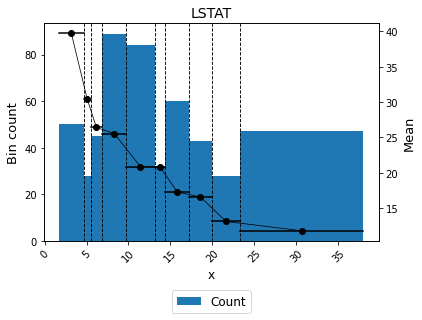
Or show the bin labels instead of bin ids.
[14]:
binning_table.plot(show_bin_labels=True)
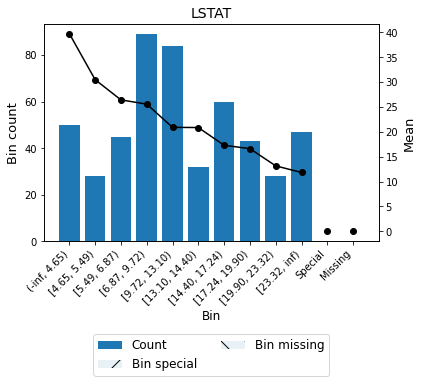
From version 0.19.0 the parameter metric is exposed to visualize other IV and WOE
[15]:
binning_table.plot(metric='iv', show_bin_labels=True)
Mean transformation¶
Now that we have checked the binned data, we can transform our original data into mean values. You can check the correctness of the transformation using pandas value_counts method, for instance.
[16]:
x_transform_bins = optb.transform(x, metric="bins")
[17]:
pd.Series(x_transform_bins).value_counts()
[17]:
[6.87, 9.72) 89
[9.72, 13.10) 84
[14.40, 17.24) 60
(-inf, 4.65) 50
[23.32, inf) 47
[5.49, 6.87) 45
[17.24, 19.90) 43
[13.10, 14.40) 32
[19.90, 23.32) 28
[4.65, 5.49) 28
dtype: int64
Advanced¶
Many of the advanced options have been covered in the previous tutorials with a binary target. Check it out! In this section, we focus on the mean monotonicity trend and the mean difference between bins.
Binning table statistical analysis¶
The analysis method performs a statistical analysis of the binning table, computing the Information Value (IV), Weight of Evidence (WoE), and Herfindahl-Hirschman Index (HHI). Additionally, several statistical significance tests between consecutive bins of the contingency table are performed using the Student’s t-test.
[18]:
binning_table.analysis()
-------------------------------------------------
OptimalBinning: Continuous Binning Table Analysis
-------------------------------------------------
General metrics
IV 6.03021763
WoE 111.65056765
WoE (normalized) 4.95502274
HHI 0.11620241
HHI (normalized) 0.03585717
Quality score 0.01333978
Monotonic trend descending
Significance tests
Bin A Bin B t-statistic p-value
0 1 5.644492 3.313748e-07
1 2 2.924528 5.175586e-03
2 3 0.808313 4.206096e-01
3 4 5.874488 3.816654e-08
4 5 0.073112 9.419504e-01
5 6 5.428848 5.770714e-07
6 7 0.883289 3.796030e-01
7 8 3.591859 6.692488e-04
8 9 1.408305 1.643801e-01
Mean monotonicity¶
The monotonic_trend option permits forcing a monotonic trend to the mean curve. The default setting “auto” should be the preferred option, however, some business constraints might require to impose different trends. The default setting “auto” chooses the monotonic trend most likely to minimize the L1-norm from the options “ascending”, “descending”, “peak” and “valley” using a machine-learning-based classifier.
[19]:
variable = "INDUS"
x = df[variable].values
[20]:
optb = ContinuousOptimalBinning(name=variable, dtype="numerical",
monotonic_trend="auto")
optb.fit(x, y)
[20]:
ContinuousOptimalBinning(name='INDUS')
[21]:
binning_table = optb.binning_table
binning_table.build()
[21]:
| Bin | Count | Count (%) | Sum | Std | Mean | Min | Max | Zeros count | WoE | IV | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | (-inf, 3.35) | 63 | 0.124506 | 1994.0 | 8.569841 | 31.650794 | 16.5 | 50.0 | 0 | 9.117987 | 1.135243 |
| 1 | [3.35, 5.04) | 57 | 0.112648 | 1615.2 | 8.072710 | 28.336842 | 17.2 | 50.0 | 0 | 5.804036 | 0.653814 |
| 2 | [5.04, 6.66) | 66 | 0.130435 | 1723.7 | 7.879078 | 26.116667 | 16.0 | 50.0 | 0 | 3.583860 | 0.467460 |
| 3 | [6.66, 9.12) | 64 | 0.126482 | 1292.0 | 4.614126 | 20.187500 | 12.7 | 35.2 | 0 | -2.345306 | 0.296640 |
| 4 | [9.12, 10.30) | 29 | 0.057312 | 584.1 | 2.252281 | 20.141379 | 16.1 | 24.5 | 0 | -2.391427 | 0.137058 |
| 5 | [10.30, 20.73) | 200 | 0.395257 | 3736.2 | 8.959305 | 18.681000 | 5.0 | 50.0 | 0 | -3.851806 | 1.522453 |
| 6 | [20.73, inf) | 27 | 0.053360 | 456.4 | 3.690878 | 16.903704 | 7.0 | 23.0 | 0 | -5.629103 | 0.300367 |
| 7 | Special | 0 | 0.000000 | 0.0 | NaN | 0.000000 | NaN | NaN | 0 | -22.532806 | 0.000000 |
| 8 | Missing | 0 | 0.000000 | 0.0 | NaN | 0.000000 | NaN | NaN | 0 | -22.532806 | 0.000000 |
| Totals | 506 | 1.000000 | 11401.6 | 22.532806 | 5.0 | 50.0 | 0 | 77.789138 | 4.513036 |
[22]:
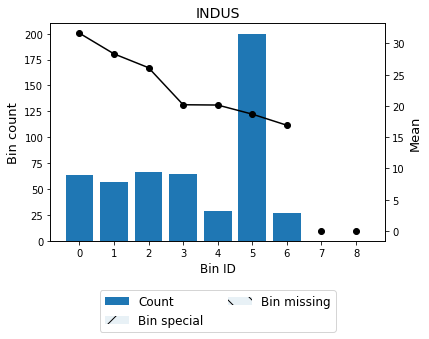
binning_table.plot()
[23]:
optb.information()
optbinning (Version 0.19.0)
Copyright (c) 2019-2024 Guillermo Navas-Palencia, Apache License 2.0
Name : INDUS
Status : OPTIMAL
Pre-binning statistics
Number of pre-bins 13
Number of refinements 0
Solver statistics
Type cp
Number of booleans 100
Number of branches 211
Number of conflicts 3
Objective value 32723523
Best objective bound 32723523
Timing
Total time 0.21 sec
Pre-processing 0.00 sec ( 0.30%)
Pre-binning 0.01 sec ( 3.20%)
Solver 0.21 sec ( 95.80%)
model generation 0.17 sec ( 84.80%)
optimizer 0.03 sec ( 15.20%)
Post-processing 0.00 sec ( 0.18%)
[24]:
binning_table.analysis()
-------------------------------------------------
OptimalBinning: Continuous Binning Table Analysis
-------------------------------------------------
General metrics
IV 4.51303567
WoE 77.78913838
WoE (normalized) 3.45226144
HHI 0.22356231
HHI (normalized) 0.12650760
Quality score 0.02383215
Monotonic trend descending
Significance tests
Bin A Bin B t-statistic p-value
0 1 2.180865 3.118080e-02
1 2 1.537968 1.267445e-01
2 3 5.254539 7.781110e-07
3 4 0.064736 9.485275e-01
4 5 1.923770 5.601023e-02
5 6 1.867339 6.563949e-02
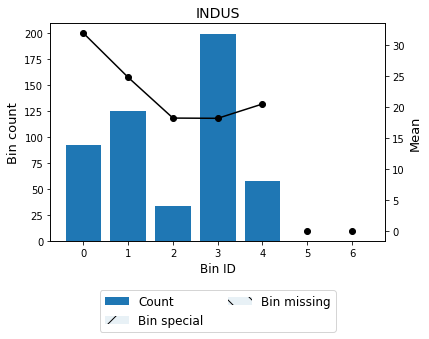
A smoother curve, keeping the valley monotonicity, can be achieved by using monotonic_trend="convex".
[25]:
optb = ContinuousOptimalBinning(name=variable, dtype="numerical",
monotonic_trend="convex")
optb.fit(x, y)
[25]:
ContinuousOptimalBinning(monotonic_trend='convex', name='INDUS')
[26]:
binning_table = optb.binning_table
binning_table.build()
[26]:
| Bin | Count | Count (%) | Sum | Std | Mean | Min | Max | Zeros count | WoE | IV | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | (-inf, 3.99) | 92 | 0.181818 | 2932.6 | 8.688703 | 31.876087 | 16.5 | 50.0 | 0 | 9.343281 | 1.698778 |
| 1 | [3.99, 8.01) | 125 | 0.247036 | 3092.3 | 6.644213 | 24.738400 | 14.4 | 50.0 | 0 | 2.205594 | 0.544860 |
| 2 | [8.01, 9.12) | 33 | 0.065217 | 600.0 | 3.614571 | 18.181818 | 12.7 | 27.5 | 0 | -4.350988 | 0.283760 |
| 3 | [9.12, 18.84) | 199 | 0.393281 | 3610.8 | 7.540328 | 18.144724 | 5.0 | 50.0 | 0 | -4.388083 | 1.725748 |
| 4 | [18.84, inf) | 57 | 0.112648 | 1165.9 | 9.519086 | 20.454386 | 7.0 | 50.0 | 0 | -2.078420 | 0.234130 |
| 5 | Special | 0 | 0.000000 | 0.0 | NaN | 0.000000 | NaN | NaN | 0 | -22.532806 | 0.000000 |
| 6 | Missing | 0 | 0.000000 | 0.0 | NaN | 0.000000 | NaN | NaN | 0 | -22.532806 | 0.000000 |
| Totals | 506 | 1.000000 | 11401.6 | 22.532806 | 5.0 | 50.0 | 0 | 67.431978 | 4.487277 |
[27]:
binning_table.plot()
[28]:
binning_table.analysis()
-------------------------------------------------
OptimalBinning: Continuous Binning Table Analysis
-------------------------------------------------
General metrics
IV 4.48727679
WoE 67.43197816
WoE (normalized) 2.99261340
HHI 0.26569701
HHI (normalized) 0.14331318
Quality score 0.01843250
Monotonic trend valley (convex)
Significance tests
Bin A Bin B t-statistic p-value
0 1 6.588254 5.789868e-10
1 2 7.575550 2.331580e-11
2 3 0.044930 9.642654e-01
3 4 -1.686553 9.572501e-02
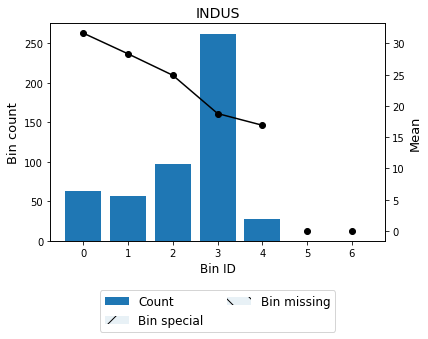
For example, we can force the variable INDUS (proportion of non-retail business acres per town) to be monotonically descending with respect to the house-pric and satisfy a max p-value constraint.
[29]:
optb = ContinuousOptimalBinning(name=variable, dtype="numerical",
monotonic_trend="descending",
max_pvalue=0.05)
optb.fit(x, y)
[29]:
ContinuousOptimalBinning(max_pvalue=0.05, monotonic_trend='descending',
name='INDUS')
[30]:
binning_table = optb.binning_table
binning_table.build()
[30]:
| Bin | Count | Count (%) | Sum | Std | Mean | Min | Max | Zeros count | WoE | IV | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | (-inf, 3.35) | 63 | 0.124506 | 1994.0 | 8.569841 | 31.650794 | 16.5 | 50.0 | 0 | 9.117987 | 1.135243 |
| 1 | [3.35, 5.04) | 57 | 0.112648 | 1615.2 | 8.072710 | 28.336842 | 17.2 | 50.0 | 0 | 5.804036 | 0.653814 |
| 2 | [5.04, 8.01) | 97 | 0.191700 | 2415.7 | 7.221288 | 24.904124 | 14.4 | 50.0 | 0 | 2.371317 | 0.454581 |
| 3 | [8.01, 20.73) | 262 | 0.517787 | 4920.3 | 7.983667 | 18.779771 | 5.0 | 50.0 | 0 | -3.753035 | 1.943271 |
| 4 | [20.73, inf) | 27 | 0.053360 | 456.4 | 3.690878 | 16.903704 | 7.0 | 23.0 | 0 | -5.629103 | 0.300367 |
| 5 | Special | 0 | 0.000000 | 0.0 | NaN | 0.000000 | NaN | NaN | 0 | -22.532806 | 0.000000 |
| 6 | Missing | 0 | 0.000000 | 0.0 | NaN | 0.000000 | NaN | NaN | 0 | -22.532806 | 0.000000 |
| Totals | 506 | 1.000000 | 11401.6 | 22.532806 | 5.0 | 50.0 | 0 | 71.741091 | 4.487277 |
[31]:
binning_table.plot()
[32]:
binning_table.analysis()
-------------------------------------------------
OptimalBinning: Continuous Binning Table Analysis
-------------------------------------------------
General metrics
IV 4.48727679
WoE 71.74109110
WoE (normalized) 3.18385070
HHI 0.33589027
HHI (normalized) 0.22520531
Quality score 0.49256380
Monotonic trend descending
Significance tests
Bin A Bin B t-statistic p-value
0 1 2.180865 3.118080e-02
1 2 2.647685 9.326789e-03
2 3 6.930572 6.470796e-11
3 4 2.169454 3.432174e-02
Mininum mean difference between consecutive bins¶
Now, we note that the mean difference between consecutive bins is not significant enough. Therefore, we decide to set min_mean_diff=1.0:
[33]:
optb = ContinuousOptimalBinning(name=variable, dtype="numerical",
monotonic_trend="descending", min_mean_diff=1.0)
optb.fit(x, y)
[33]:
ContinuousOptimalBinning(min_mean_diff=1.0, monotonic_trend='descending',
name='INDUS')
[34]:
binning_table = optb.binning_table
binning_table.build()
[34]:
| Bin | Count | Count (%) | Sum | Std | Mean | Min | Max | Zeros count | WoE | IV | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | (-inf, 3.35) | 63 | 0.124506 | 1994.0 | 8.569841 | 31.650794 | 16.5 | 50.0 | 0 | 9.117987 | 1.135243 |
| 1 | [3.35, 5.04) | 57 | 0.112648 | 1615.2 | 8.072710 | 28.336842 | 17.2 | 50.0 | 0 | 5.804036 | 0.653814 |
| 2 | [5.04, 6.66) | 66 | 0.130435 | 1723.7 | 7.879078 | 26.116667 | 16.0 | 50.0 | 0 | 3.583860 | 0.467460 |
| 3 | [6.66, 10.30) | 93 | 0.183794 | 1876.1 | 4.029092 | 20.173118 | 12.7 | 35.2 | 0 | -2.359688 | 0.433698 |
| 4 | [10.30, 20.73) | 200 | 0.395257 | 3736.2 | 8.959305 | 18.681000 | 5.0 | 50.0 | 0 | -3.851806 | 1.522453 |
| 5 | [20.73, inf) | 27 | 0.053360 | 456.4 | 3.690878 | 16.903704 | 7.0 | 23.0 | 0 | -5.629103 | 0.300367 |
| 6 | Special | 0 | 0.000000 | 0.0 | NaN | 0.000000 | NaN | NaN | 0 | -22.532806 | 0.000000 |
| 7 | Missing | 0 | 0.000000 | 0.0 | NaN | 0.000000 | NaN | NaN | 0 | -22.532806 | 0.000000 |
| Totals | 506 | 1.000000 | 11401.6 | 22.532806 | 5.0 | 50.0 | 0 | 75.412093 | 4.513036 |
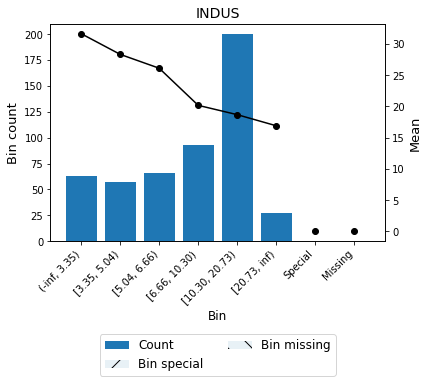
[35]:
binning_table.plot(show_bin_labels=True)
[36]:
binning_table.analysis()
-------------------------------------------------
OptimalBinning: Continuous Binning Table Analysis
-------------------------------------------------
General metrics
IV 4.51303567
WoE 75.41209309
WoE (normalized) 3.34676880
HHI 0.23806027
HHI (normalized) 0.12921174
Quality score 0.45843318
Monotonic trend descending
Significance tests
Bin A Bin B t-statistic p-value
0 1 2.180865 3.118080e-02
1 2 1.537968 1.267445e-01
2 3 5.628303 2.077284e-07
3 4 1.966209 5.022562e-02
4 5 1.867339 6.563949e-02
Handle outliers¶
Version 0.16.1 introduced the outlier detector YQuantileDetector, specially designed to remove outliers for the ContinuousOptimalBinning algorithm. The application of this detector permits obtaining mean values per bin more similar to those obtained with more robust statistics (e.g., the median).
[37]:
from optbinning.binning.outlier import YQuantileDetector
[38]:
variable = "LSTAT"
x = df[variable].values
[39]:
detector = YQuantileDetector(n_bins=10, outlier_detector="range",
outlier_params={'method': 'HDI'})
detector.fit(x, y)
[39]:
YQuantileDetector(n_bins=10, outlier_detector='range',
outlier_params={'method': 'HDI'})
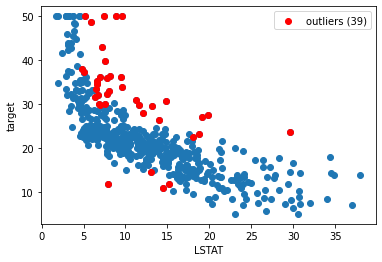
[40]:
plt.scatter(x, y)
mask = detector.get_support()
plt.scatter(x[mask], y[mask], color='r', label=f"outliers ({np.count_nonzero(mask)})")
plt.xlabel(variable)
plt.ylabel("target")
plt.legend()
plt.show()
[41]:
optb = ContinuousOptimalBinning(name=variable, dtype="numerical",
monotonic_trend="descending",
outlier_detector="yquantile",
outlier_params={
'n_bins': 10,
'outlier_detector': 'range',
'outlier_params': {'method': 'HDI'}
},
verbose=True)
optb.fit(x, y)
2024-01-15 00:07:47,337 | INFO : Optimal binning started.
2024-01-15 00:07:47,339 | INFO : Options: check parameters.
2024-01-15 00:07:47,340 | INFO : Pre-processing started.
2024-01-15 00:07:47,341 | INFO : Pre-processing: number of samples: 506
2024-01-15 00:07:47,345 | INFO : Pre-processing: number of clean samples: 467
2024-01-15 00:07:47,346 | INFO : Pre-processing: number of missing samples: 0
2024-01-15 00:07:47,347 | INFO : Pre-processing: number of special samples: 0
2024-01-15 00:07:47,348 | INFO : Pre-processing: number of outlier samples: 39
2024-01-15 00:07:47,349 | INFO : Pre-processing terminated. Time: 0.0034s
2024-01-15 00:07:47,350 | INFO : Pre-binning started.
2024-01-15 00:07:47,357 | INFO : Pre-binning: number of prebins: 14
2024-01-15 00:07:47,359 | INFO : Pre-binning terminated. Time: 0.0059s
2024-01-15 00:07:47,360 | INFO : Optimizer started.
2024-01-15 00:07:47,361 | INFO : Optimizer: monotonic trend set to descending.
2024-01-15 00:07:47,362 | INFO : Optimizer: build model...
2024-01-15 00:07:47,498 | INFO : Optimizer: solve...
2024-01-15 00:07:47,526 | INFO : Optimizer terminated. Time: 0.1650s
2024-01-15 00:07:47,528 | INFO : Post-processing started.
2024-01-15 00:07:47,529 | INFO : Post-processing: compute binning information.
2024-01-15 00:07:47,532 | INFO : Post-processing terminated. Time: 0.0020s
2024-01-15 00:07:47,533 | INFO : Optimal binning terminated. Status: OPTIMAL. Time: 0.1960s
[41]:
ContinuousOptimalBinning(monotonic_trend='descending', name='LSTAT',
outlier_detector='yquantile',
outlier_params={'n_bins': 10,
'outlier_detector': 'range',
'outlier_params': {'method': 'HDI'}},
verbose=True)
[42]:
optb.binning_table.build()
[42]:
| Bin | Count | Count (%) | Sum | Std | Mean | Min | Max | Zeros count | WoE | IV | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | (-inf, 4.15) | 36 | 0.077088 | 1495.8 | 7.729866 | 41.550000 | 24.8 | 50.0 | 0 | 19.824732 | 1.528245 |
| 1 | [4.15, 5.49) | 39 | 0.083512 | 1218.2 | 6.428482 | 31.235897 | 21.9 | 50.0 | 0 | 9.510630 | 0.794250 |
| 2 | [5.49, 6.57) | 29 | 0.062099 | 735.1 | 3.174426 | 25.348276 | 20.6 | 33.2 | 0 | 3.623008 | 0.224983 |
| 3 | [6.57, 7.68) | 29 | 0.062099 | 705.8 | 2.035786 | 24.337931 | 20.7 | 29.1 | 0 | 2.612663 | 0.162242 |
| 4 | [7.68, 9.95) | 59 | 0.126338 | 1341.0 | 3.012688 | 22.728814 | 16.5 | 30.3 | 0 | 1.003546 | 0.126786 |
| 5 | [9.95, 11.67) | 42 | 0.089936 | 884.4 | 2.257068 | 21.057143 | 15.0 | 24.7 | 0 | -0.668125 | 0.060088 |
| 6 | [11.67, 13.74) | 49 | 0.104925 | 982.4 | 2.119503 | 20.048980 | 15.0 | 24.5 | 0 | -1.676288 | 0.175885 |
| 7 | [13.74, 15.00) | 28 | 0.059957 | 550.2 | 2.143012 | 19.650000 | 16.0 | 24.4 | 0 | -2.075268 | 0.124427 |
| 8 | [15.00, 17.11) | 37 | 0.079229 | 632.6 | 2.794830 | 17.097297 | 10.2 | 22.4 | 0 | -4.627970 | 0.366670 |
| 9 | [17.11, 18.93) | 38 | 0.081370 | 607.3 | 2.970810 | 15.981579 | 9.6 | 23.1 | 0 | -5.743689 | 0.467367 |
| 10 | [18.93, 21.95) | 26 | 0.055675 | 350.5 | 3.532271 | 13.480769 | 7.2 | 21.7 | 0 | -8.244498 | 0.459008 |
| 11 | [21.95, 26.44) | 27 | 0.057816 | 332.0 | 3.524148 | 12.296296 | 5.0 | 20.0 | 0 | -9.428971 | 0.545144 |
| 12 | [26.44, inf) | 28 | 0.059957 | 310.4 | 3.754589 | 11.085714 | 5.0 | 17.9 | 0 | -10.639553 | 0.637918 |
| 13 | Special | 0 | 0.000000 | 0.0 | NaN | 0.000000 | NaN | NaN | 0 | -21.725268 | 0.000000 |
| 14 | Missing | 0 | 0.000000 | 0.0 | NaN | 0.000000 | NaN | NaN | 0 | -21.725268 | 0.000000 |
| Totals | 467 | 1.000000 | 10145.7 | 21.725268 | 5.0 | 50.0 | 0 | 123.129478 | 5.673013 |
[43]:
optb.binning_table.plot()
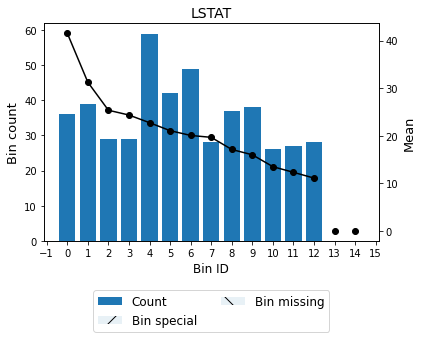
As observed in the logs, 39 outliers were removed during preprocessing. Compared to the standard binning, the resulting binning after removing outliers returns more bins (13 vs 10) and higher objective function (total WoE).
Sample weights¶
Finally, version 0.17.0 added support to sample weights. As an example, let’s increase the weights for values < 10.
[44]:
sample_weight = np.ones(len(x))
sample_weight[x < 10] = 5
[45]:
optb = ContinuousOptimalBinning(name=variable, dtype="numerical",
monotonic_trend="descending")
optb.fit(x, y, sample_weight=sample_weight)
[45]:
ContinuousOptimalBinning(monotonic_trend='descending', name='LSTAT')
[46]:
optb.binning_table.build()
[46]:
| Bin | Count | Count (%) | Sum | Std | Mean | Min | Max | Zeros count | WoE | IV | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | (-inf, 4.15) | 180 | 0.130246 | 7479.0 | 84.878526 | 41.550000 | 124.0 | 250.0 | 0 | 14.617149 | 1.903825 |
| 1 | [4.15, 5.15) | 155 | 0.112156 | 5135.0 | 68.222852 | 33.129032 | 112.5 | 250.0 | 0 | 6.196181 | 0.694941 |
| 2 | [5.15, 6.06) | 140 | 0.101302 | 3850.5 | 56.552267 | 27.503571 | 103.0 | 244.0 | 0 | 0.570720 | 0.057815 |
| 3 | [6.06, 6.87) | 140 | 0.101302 | 3674.0 | 53.287277 | 26.242857 | 103.5 | 176.0 | 0 | -0.689994 | 0.069898 |
| 4 | [6.87, 8.85) | 285 | 0.206223 | 7275.0 | 53.081171 | 25.526316 | 59.5 | 250.0 | 0 | -1.406535 | 0.290060 |
| 5 | [8.85, 9.95) | 185 | 0.133864 | 4663.0 | 52.840208 | 25.205405 | 93.5 | 250.0 | 0 | -1.727446 | 0.231243 |
| 6 | [9.95, 11.67) | 52 | 0.037627 | 1103.6 | 17.592652 | 21.223077 | 15.0 | 101.5 | 0 | -5.709774 | 0.214840 |
| 7 | [11.67, 14.40) | 67 | 0.048480 | 1364.9 | 2.652276 | 20.371642 | 14.5 | 29.6 | 0 | -6.561209 | 0.318090 |
| 8 | [14.40, 17.24) | 60 | 0.043415 | 1037.5 | 3.588003 | 17.291667 | 10.2 | 30.7 | 0 | -9.641184 | 0.418575 |
| 9 | [17.24, 19.90) | 43 | 0.031114 | 714.3 | 4.032554 | 16.611628 | 8.3 | 27.5 | 0 | -10.321223 | 0.321138 |
| 10 | [19.90, 23.32) | 28 | 0.020260 | 368.4 | 3.912839 | 13.157143 | 5.0 | 21.7 | 0 | -13.775708 | 0.279103 |
| 11 | [23.32, inf) | 47 | 0.034009 | 556.0 | 4.006586 | 11.829787 | 5.0 | 23.7 | 0 | -15.103064 | 0.513635 |
| 12 | Special | 0 | 0.000000 | 0.0 | NaN | 0.000000 | NaN | NaN | 0 | -26.932851 | 0.000000 |
| 13 | Missing | 0 | 0.000000 | 0.0 | NaN | 0.000000 | NaN | NaN | 0 | -26.932851 | 0.000000 |
| Totals | 1382 | 1.000000 | 37221.2 | 26.932851 | 5.0 | 250.0 | 0 | 140.185889 | 5.313163 |
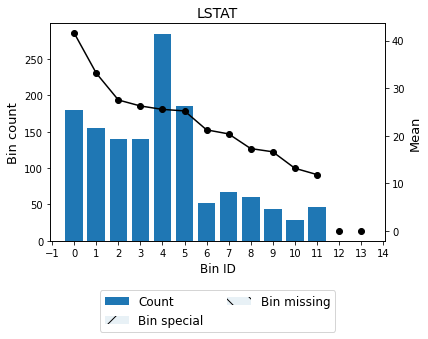
Note the count increase in the first bins.
[47]:
optb.binning_table.plot()