Tutorial: optimal binning with multiclass target¶
Basic¶
To get us started, let’s load a well-known dataset from the UCI repository and transform the data into a pandas.DataFrame.
[1]:
import pandas as pd
from sklearn.datasets import load_wine
[2]:
data = load_wine()
df = pd.DataFrame(data.data, columns=data.feature_names)
We choose a variable to discretize and the multiclass target.
[3]:
variable = "ash"
x = df[variable].values
y = data.target
Import and instantiate an MulticlassOptimalBinning object class. We pass the variable name and a solver, in this case, we choose the constraint programming solver.
[4]:
from optbinning import MulticlassOptimalBinning
[5]:
optb = MulticlassOptimalBinning(name=variable, solver="cp")
We fit the optimal binning object with arrays x and y.
[6]:
optb.fit(x, y)
[6]:
MulticlassOptimalBinning(name='ash')
You can check if an optimal solution has been found via the status attribute:
[7]:
optb.status
[7]:
'OPTIMAL'
You can also retrieve the optimal split points via the splits attribute:
[8]:
optb.splits
[8]:
array([2.1450001 , 2.245 , 2.31499994, 2.6049999 , 2.6450001 ])
The binning table¶
The optimal binning algorithms return a binning table; a binning table displays the binned data and several metrics for each bin. Class OptimalBinning returns an object MulticlassBinningTable via the binning_table attribute.
[9]:
binning_table = optb.binning_table
[10]:
type(binning_table)
[10]:
optbinning.binning.binning_statistics.MulticlassBinningTable
The binning_table is instantiated, but not built. Therefore, the first step is to call the method build, which returns a pandas.DataFrame.
[11]:
binning_table.build()
[11]:
| Bin | Count | Count (%) | Event_0 | Event_1 | Event_2 | Event_rate_0 | Event_rate_1 | Event_rate_2 | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | (-inf, 2.15) | 31 | 0.174157 | 7 | 23 | 1 | 0.225806 | 0.741935 | 0.032258 |
| 1 | [2.15, 2.25) | 20 | 0.112360 | 2 | 13 | 5 | 0.100000 | 0.650000 | 0.250000 |
| 2 | [2.25, 2.31) | 26 | 0.146067 | 9 | 10 | 7 | 0.346154 | 0.384615 | 0.269231 |
| 3 | [2.31, 2.60) | 64 | 0.359551 | 24 | 17 | 23 | 0.375000 | 0.265625 | 0.359375 |
| 4 | [2.60, 2.65) | 10 | 0.056180 | 4 | 1 | 5 | 0.400000 | 0.100000 | 0.500000 |
| 5 | [2.65, inf) | 27 | 0.151685 | 13 | 7 | 7 | 0.481481 | 0.259259 | 0.259259 |
| 6 | Special | 0 | 0.000000 | 0 | 0 | 0 | 0.000000 | 0.000000 | 0.000000 |
| 7 | Missing | 0 | 0.000000 | 0 | 0 | 0 | 0.000000 | 0.000000 | 0.000000 |
| Totals | 178 | 1.000000 | 59 | 71 | 48 | 0.331461 | 0.398876 | 0.269663 |
Let’s describe the columns of this binning table:
Bin: the intervals delimited by the optimal split points.
Count: the number of records for each bin.
Count (%): the percentage of records for each bin.
Event: the number of event records \((y = class)\) for each bin.
Event rate: the percentage of event records for each bin. This is computed using one-vs-all or one-vs-rest approach.
The last row shows the total number of records, event records, and event rates.
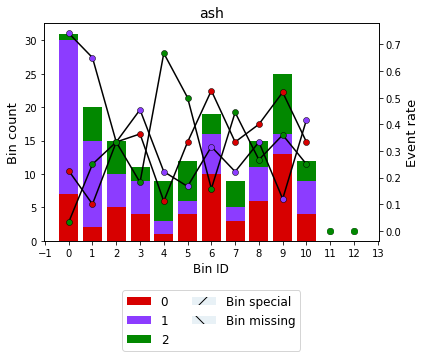
You can use the method plot to visualize the histogram and event rate curve. Note that the Bin ID corresponds to the binning table index.
[12]:
binning_table.plot()
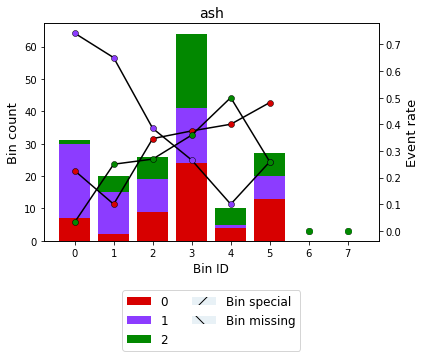
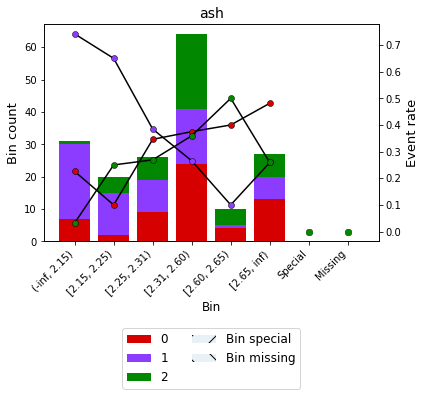
Alternatively, the Bin can be visualized using show_bin_labels=True (since version 0.15.1)
[13]:
binning_table.plot(show_bin_labels=True)
Transformation¶
Now that we have checked the binned data, we can transform our original data into a measure based on the one-vs-rest WoE metric. You can check the correctness of the transformation using pandas value_counts method, for instance.
[14]:
x_transform_woe = optb.transform(x, metric="bins")
[15]:
pd.Series(x_transform_woe).value_counts()
[15]:
[2.31, 2.60) 64
(-inf, 2.15) 31
[2.65, inf) 27
[2.25, 2.31) 26
[2.15, 2.25) 20
[2.60, 2.65) 10
dtype: int64
Advanced¶
Many of the advanced options have been covered in the previous tutorials with a binary target. Check it out! In this section, we focus on the binning table statistical analysis and the event rate monotonicity trends.
Binning table statistical analysis¶
The analysis method performs a statistical analysis of the binning table, computing the Jensen-shannon divergence and the quality score. Additionally, a statistical significance test between consecutive bins of the contingency table is performed using the Chi-square test.
[16]:
binning_table.analysis()
-------------------------------------------------
OptimalBinning: Multiclass Binning Table Analysis
-------------------------------------------------
General metrics
JS (Jensen-Shannon) 0.10989515
HHI 0.21973236
HHI (normalized) 0.10826555
Cramer's V 0.31694075
Quality score 0.05279822
Monotonic trend
Class 0 valley
Class 1 valley
Class 2 peak
Significance tests
Bin A Bin B t-statistic p-value
0 1 6.135081 0.046535
1 2 4.472669 0.106849
2 3 1.365275 0.505282
3 4 1.441642 0.486353
4 5 2.265477 0.322150
Event rate monotonicity¶
The monotonic_trend option permits forcing a monotonic trend to the event rate curve of each class. The default setting “auto” should be the preferred option, however, some business constraints might require to impose different trends. The default setting “auto” chooses the monotonic trend most likely to maximize the information value from the options “ascending”, “descending”, “peak” and “valley” for each class using a machine-learning-based classifier.
A good starting point to decide which monotonic trend to enforce for each class is to use monotonic_trend=None.
[17]:
optb = MulticlassOptimalBinning(name=variable, solver="mip", monotonic_trend=None)
optb.fit(x, y)
[17]:
MulticlassOptimalBinning(monotonic_trend=None, name='ash', solver='mip')
[18]:
binning_table = optb.binning_table
binning_table.build()
[18]:
| Bin | Count | Count (%) | Event_0 | Event_1 | Event_2 | Event_rate_0 | Event_rate_1 | Event_rate_2 | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | (-inf, 2.15) | 31 | 0.174157 | 7 | 23 | 1 | 0.225806 | 0.741935 | 0.032258 |
| 1 | [2.15, 2.25) | 20 | 0.112360 | 2 | 13 | 5 | 0.100000 | 0.650000 | 0.250000 |
| 2 | [2.25, 2.28) | 15 | 0.084270 | 5 | 5 | 5 | 0.333333 | 0.333333 | 0.333333 |
| 3 | [2.28, 2.31) | 11 | 0.061798 | 4 | 5 | 2 | 0.363636 | 0.454545 | 0.181818 |
| 4 | [2.31, 2.35) | 9 | 0.050562 | 1 | 2 | 6 | 0.111111 | 0.222222 | 0.666667 |
| 5 | [2.35, 2.39) | 12 | 0.067416 | 4 | 2 | 6 | 0.333333 | 0.166667 | 0.500000 |
| 6 | [2.39, 2.47) | 19 | 0.106742 | 10 | 6 | 3 | 0.526316 | 0.315789 | 0.157895 |
| 7 | [2.47, 2.50) | 9 | 0.050562 | 3 | 2 | 4 | 0.333333 | 0.222222 | 0.444444 |
| 8 | [2.50, 2.60) | 15 | 0.084270 | 6 | 5 | 4 | 0.400000 | 0.333333 | 0.266667 |
| 9 | [2.60, 2.65) | 10 | 0.056180 | 4 | 1 | 5 | 0.400000 | 0.100000 | 0.500000 |
| 10 | [2.65, 2.73) | 15 | 0.084270 | 9 | 2 | 4 | 0.600000 | 0.133333 | 0.266667 |
| 11 | [2.73, inf) | 12 | 0.067416 | 4 | 5 | 3 | 0.333333 | 0.416667 | 0.250000 |
| 12 | Special | 0 | 0.000000 | 0 | 0 | 0 | 0.000000 | 0.000000 | 0.000000 |
| 13 | Missing | 0 | 0.000000 | 0 | 0 | 0 | 0.000000 | 0.000000 | 0.000000 |
| Totals | 178 | 1.000000 | 59 | 71 | 48 | 0.331461 | 0.398876 | 0.269663 |
[19]:
binning_table.plot()
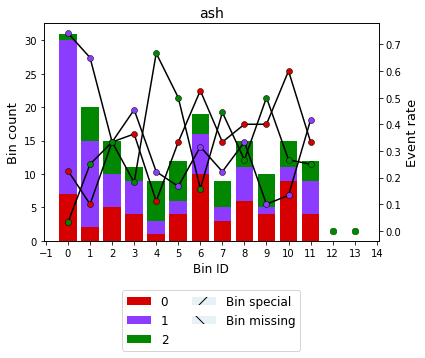
[20]:
binning_table.analysis()
-------------------------------------------------
OptimalBinning: Multiclass Binning Table Analysis
-------------------------------------------------
General metrics
JS (Jensen-Shannon) 0.15199204
HHI 0.09683121
HHI (normalized) 0.02735669
Cramer's V 0.37833165
Quality score 0.00403065
Monotonic trend
Class 0 no monotonic
Class 1 no monotonic
Class 2 no monotonic
Significance tests
Bin A Bin B t-statistic p-value
0 1 6.135081 0.046535
1 2 4.212963 0.121665
2 3 0.800385 0.670191
3 4 4.935065 0.084794
4 5 1.400000 0.496585
5 6 4.205201 0.122138
6 7 2.682861 0.261471
7 8 0.838095 0.657673
8 9 2.268519 0.321660
9 10 1.424501 0.490539
10 11 3.056044 0.216964
For example, we can decide that we do not care about class 2 and only force classes 0 and 1.
[21]:
optb = MulticlassOptimalBinning(name=variable, solver="mip",
monotonic_trend=["ascending", "auto", None],
verbose=True)
optb.fit(x, y)
2024-01-15 00:17:04,003 | INFO : Optimal binning started.
2024-01-15 00:17:04,007 | INFO : Options: check parameters.
2024-01-15 00:17:04,009 | INFO : Pre-processing started.
2024-01-15 00:17:04,010 | INFO : Pre-processing: number of samples: 178
2024-01-15 00:17:04,012 | INFO : Pre-processing: number of clean samples: 178
2024-01-15 00:17:04,013 | INFO : Pre-processing: number of missing samples: 0
2024-01-15 00:17:04,015 | INFO : Pre-processing: number of special samples: 0
2024-01-15 00:17:04,016 | INFO : Pre-processing terminated. Time: 0.0002s
2024-01-15 00:17:04,017 | INFO : Pre-binning started.
2024-01-15 00:17:04,026 | INFO : Pre-binning: number prebins removed: 1
2024-01-15 00:17:04,028 | INFO : Pre-binning: number of prebins: 12
2024-01-15 00:17:04,031 | INFO : Pre-binning: number of refinements: 1
2024-01-15 00:17:04,032 | INFO : Pre-binning terminated. Time: 0.0097s
2024-01-15 00:17:04,034 | INFO : Optimizer started.
2024-01-15 00:17:04,039 | INFO : Optimizer: classifier predicts valley monotonic trend.
2024-01-15 00:17:04,040 | INFO : Optimizer: build model...
2024-01-15 00:17:04,241 | INFO : Optimizer: solve...
2024-01-15 00:17:04,248 | INFO : Optimizer terminated. Time: 0.2129s
2024-01-15 00:17:04,250 | INFO : Post-processing started.
2024-01-15 00:17:04,252 | INFO : Post-processing: compute binning information.
2024-01-15 00:17:04,254 | INFO : Post-processing terminated. Time: 0.0004s
2024-01-15 00:17:04,260 | INFO : Optimal binning terminated. Status: OPTIMAL. Time: 0.2568s
[21]:
MulticlassOptimalBinning(monotonic_trend=['ascending', 'auto', None],
name='ash', solver='mip', verbose=True)
[22]:
binning_table = optb.binning_table
binning_table.build()
[22]:
| Bin | Count | Count (%) | Event_0 | Event_1 | Event_2 | Event_rate_0 | Event_rate_1 | Event_rate_2 | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | (-inf, 2.25) | 51 | 0.286517 | 9 | 36 | 6 | 0.176471 | 0.705882 | 0.117647 |
| 1 | [2.25, 2.35) | 35 | 0.196629 | 10 | 12 | 13 | 0.285714 | 0.342857 | 0.371429 |
| 2 | [2.35, 2.39) | 12 | 0.067416 | 4 | 2 | 6 | 0.333333 | 0.166667 | 0.500000 |
| 3 | [2.39, inf) | 80 | 0.449438 | 36 | 21 | 23 | 0.450000 | 0.262500 | 0.287500 |
| 4 | Special | 0 | 0.000000 | 0 | 0 | 0 | 0.000000 | 0.000000 | 0.000000 |
| 5 | Missing | 0 | 0.000000 | 0 | 0 | 0 | 0.000000 | 0.000000 | 0.000000 |
| Totals | 178 | 1.000000 | 59 | 71 | 48 | 0.331461 | 0.398876 | 0.269663 |
[23]:
binning_table.plot()
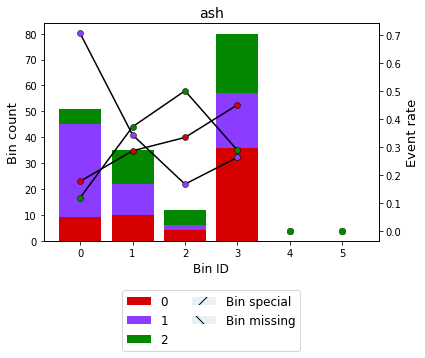
[24]:
binning_table.analysis()
-------------------------------------------------
OptimalBinning: Multiclass Binning Table Analysis
-------------------------------------------------
General metrics
JS (Jensen-Shannon) 0.08899633
HHI 0.32729453
HHI (normalized) 0.19275344
Cramer's V 0.30518651
Quality score 0.08792312
Monotonic trend
Class 0 ascending
Class 1 valley (convex)
Class 2 peak (concave)
Significance tests
Bin A Bin B t-statistic p-value
0 1 12.072711 0.002390
1 2 1.364733 0.505419
2 3 2.204828 0.332069
Event rate minimum difference¶
Since version 0.17.0, the parameter min_event_rate_diff is available for multiclass binning.
[25]:
optb = MulticlassOptimalBinning(name=variable, solver="mip",
monotonic_trend=None,
min_event_rate_diff=0.03)
optb.fit(x, y)
[25]:
MulticlassOptimalBinning(min_event_rate_diff=0.03, monotonic_trend=None,
name='ash', solver='mip')
[26]:
optb.information(print_level=2)
optbinning (Version 0.19.0)
Copyright (c) 2019-2024 Guillermo Navas-Palencia, Apache License 2.0
Begin options
name ash * U
prebinning_method cart * d
solver mip * U
max_n_prebins 20 * d
min_prebin_size 0.05 * d
min_n_bins no * d
max_n_bins no * d
min_bin_size no * d
max_bin_size no * d
monotonic_trend no * U
min_event_rate_diff 0.03 * U
max_pvalue no * d
max_pvalue_policy consecutive * d
user_splits no * d
user_splits_fixed no * d
special_codes no * d
split_digits no * d
mip_solver bop * d
time_limit 100 * d
verbose False * d
End options
Name : ash
Status : OPTIMAL
Pre-binning statistics
Number of pre-bins 12
Number of refinements 1
Solver statistics
Type mip
Number of variables 196
Number of constraints 78
Objective value 2.2657
Best objective bound 2.2657
Timing
Total time 0.05 sec
Pre-processing 0.00 sec ( 0.27%)
Pre-binning 0.00 sec ( 9.86%)
Solver 0.04 sec ( 88.28%)
Post-processing 0.00 sec ( 0.55%)
[27]:
binning_table = optb.binning_table
binning_table.build()
[27]:
| Bin | Count | Count (%) | Event_0 | Event_1 | Event_2 | Event_rate_0 | Event_rate_1 | Event_rate_2 | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | (-inf, 2.15) | 31 | 0.174157 | 7 | 23 | 1 | 0.225806 | 0.741935 | 0.032258 |
| 1 | [2.15, 2.25) | 20 | 0.112360 | 2 | 13 | 5 | 0.100000 | 0.650000 | 0.250000 |
| 2 | [2.25, 2.28) | 15 | 0.084270 | 5 | 5 | 5 | 0.333333 | 0.333333 | 0.333333 |
| 3 | [2.28, 2.31) | 11 | 0.061798 | 4 | 5 | 2 | 0.363636 | 0.454545 | 0.181818 |
| 4 | [2.31, 2.35) | 9 | 0.050562 | 1 | 2 | 6 | 0.111111 | 0.222222 | 0.666667 |
| 5 | [2.35, 2.39) | 12 | 0.067416 | 4 | 2 | 6 | 0.333333 | 0.166667 | 0.500000 |
| 6 | [2.39, 2.47) | 19 | 0.106742 | 10 | 6 | 3 | 0.526316 | 0.315789 | 0.157895 |
| 7 | [2.47, 2.50) | 9 | 0.050562 | 3 | 2 | 4 | 0.333333 | 0.222222 | 0.444444 |
| 8 | [2.50, 2.60) | 15 | 0.084270 | 6 | 5 | 4 | 0.400000 | 0.333333 | 0.266667 |
| 9 | [2.60, 2.73) | 25 | 0.140449 | 13 | 3 | 9 | 0.520000 | 0.120000 | 0.360000 |
| 10 | [2.73, inf) | 12 | 0.067416 | 4 | 5 | 3 | 0.333333 | 0.416667 | 0.250000 |
| 11 | Special | 0 | 0.000000 | 0 | 0 | 0 | 0.000000 | 0.000000 | 0.000000 |
| 12 | Missing | 0 | 0.000000 | 0 | 0 | 0 | 0.000000 | 0.000000 | 0.000000 |
| Totals | 178 | 1.000000 | 59 | 71 | 48 | 0.331461 | 0.398876 | 0.269663 |
[28]:
binning_table.plot()